Regression and Presenting Your Result

Bella Ratmelia

Today’s Outline

1. Recap: The various packages for tables
2. Simple Linear Regression in R
3. Binary Logistic Regression in R
4. (if time permits) Coding your analysis and writing your report in one place with Quarto.

Open your project - the (possibly) easier way

1. Go to the folder where you put your project for this workshop

2. Find a file with .Rproj extension - this is the R project file that holds all the information about your project.

3. Double click on the file. Rstudio should launch with your project loaded! This should be easier to ensure that you are loading the correct project when opening Rstudio.

Install and load extra packages we need today

1. Type the following line in your R console (bottom left section). Type them one by one.

   • install.packages("apaTables")
   • install.packages("huxtable")
   • install.packages("gtsummary")
   • install.packages("car")

2. Create a new R script called session-5.R

3. Paste the following lines into the script:

# loading the packages
library(apaTables)
library(huxtable)
library(gtsummary)
library(car)
library(tidyverse)

Load our data for today!

# read the CSV with WVS data
wvs_cleaned <- read_csv("data-output/wvs_cleaned_v1.csv")

# Convert categorical variables to factors
columns_to_convert <- c("country", "religiousity", "sex", "marital_status", "employment", "age_group")

wvs_cleaned <- wvs_cleaned |> 
    mutate(across(all_of(columns_to_convert), as_factor))

# peek at the data, pay attention to the data types!
glimpse(wvs_cleaned)

Recap: The various packages for tables

From last week: apaTables

apaTables is a package that will generate APA-formatted report table for correlation, ANOVA, and regression. It has limited customisations and few varity of tables. The documentation online is for the “development” version which is not what we will get if we install normally with install.packages(), so we need to rely on the vignette more. View the documentation here

Example: get the correlation table for political_scale, life_satisfaction, and financial_satisfaction

library(apaTables)

wvs_cleaned |> 
    select(life_satisfaction, financial_satisfaction, political_scale) |> 
    apa.cor.table( table.number = 1, filename = "fig-output/table-cor.doc")

This code will create a word document with the tables already formatted in APA style inside.

From last week: gtsummary

Another popular packages is gt (stands for “great tables”) and its ‘add-on’, gtsummary. It has lots of customizations (which can get overwhelming!) but fortunately the documentation is pretty good and there are plenty of code samples. View the documentation here

Example: get the mean differences table for political_scale, life_satisfaction, and financial_satisfaction, grouped by sex

library(gtsummary)

wvs_cleaned |> 
    dplyr::select(life_satisfaction, financial_satisfaction, political_scale, sex) |> 
    tbl_summary(by = sex) |> 
    add_difference()

From last week: gtsummary

Characteristic	Male N = 3,1711	Female N = 3,2321	Difference2	95% CI2,3	p-value2
life_satisfaction	7.00 (6.00, 8.00)	7.00 (6.00, 8.00)	-0.02	-0.11, 0.07	0.7
financial_satisfaction	7.00 (5.00, 8.00)	7.00 (5.00, 8.00)	0.07	-0.04, 0.17	0.2
political_scale	5.00 (4.00, 7.00)	5.00 (4.00, 6.00)	0.44	0.34, 0.54	<0.001
1 Median (Q1, Q3)
2 Welch Two Sample t-test
3 CI = Confidence Interval

How to save gtsummary() tables

1. The tables will be displayed under the “Viewer” tab on the lower right hand side of Rstudio.
2. Select the entire tables, and then copy it with Ctrl + C (or Cmd + C on Macbook)
3. Paste the table with Ctrl + V (or Cmd + V on Macbook) to your word document or Google doc.

Simple Linear Regression

Simple Linear Regression: what is it?

Linear regression is a statistical method used to model the relationship between a dependent variable (outcome) and one or more independent variables (predictors) by fitting a linear equation to the observed data. The math formula looks like this:

\[ Y = \beta_0 + \beta_1X + \varepsilon \]

• \(Y\) - the dependent variable; must be continuous
• \(X\) - the independent variable (if there are more than one, there will be \(X_1\) , \(X_2\) , and so on. This can be ordinal, nominal, or continuous
• \(\beta_0\) - the y-intercept. Represents the expected value of independent variable \(Y\) when independent variable(s) \(X\) are set to zero.
• \(\beta_1\) - the slope / coefficient for independent variable
• \(\varepsilon\) - the error term. (In some examples you might see this omitted from the formula).

Examples:

• Does a person’s age affect their life satisfaction?
• Do a person’s age and country affect their life satisfaction?

Linear Regression: One continuous predictor

Research Question: Does a person’s age influence their life satisfaction?

• The outcome/DV (\(Y\)): life_satisfaction
• The predictor/IV (\(X\)): age

life_model1 <- lm(life_satisfaction ~ age, data = wvs_cleaned)
summary(life_model1) #summarize the result

Call:
lm(formula = life_satisfaction ~ age, data = wvs_cleaned)

Residuals:
    Min      1Q  Median      3Q     Max 
-6.6563 -0.9265  0.2681  1.1546  3.3816 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 6.326442   0.067792   93.32   <2e-16 ***
age         0.016218   0.001335   12.15   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.786 on 6401 degrees of freedom
Multiple R-squared:  0.02255,   Adjusted R-squared:  0.0224 
F-statistic: 147.7 on 1 and 6401 DF,  p-value: < 2.2e-16

• Call: the formula

• Residuals: overview on the distribution of residuals (expected value minus observed value) – we can plot this to check for homoscedasticity

• Coefficients: shows the intercept, the regression coefficients for the predictor variables, and their statistical significance

• Residual standard error: the average difference between observed and expected outcome by the model. Generally the lower, the better.

• R-squared & Adjusted R-squared: indicates the proportion of variation in the outcome that can be explained by the model (i.e. goodness of fit).

• F-statistics: indicates whether the model as a whole is statistically significant and whether it explains more variance than just the baseline (intercept-only) model.

Narrating the results

Here is one possible way to narrate your result:

A linear regression analysis was conducted to assess the influence of age on life satisfaction in Canada, Singapore, and New Zealand. Age is a statistically significant but weak predictor (B = 0.016, SE = 0.001, p < 0.001), indicating that for each additional year of age, the life satisfaction is increased by 0.016 units.

The model was statistically significant (F(1, 6401) = 147.7, p < 0.001) and explained approximately 2% of the variance in life satisfaction (R² = 0.022, Adjusted R² = 0.0224).

Present your regression result - huxtable

huxreg("life satisfaction" = life_model1)

	life satisfaction
(Intercept)	6.326 ***
	(0.068)
age	0.016 ***
	(0.001)
N	6403
R2	0.023
logLik	-12796.748
AIC	25599.496
*** p < 0.001; ** p < 0.01; * p < 0.05.

Linear Regression: Multiple continuous predictors

Research Question: Do a person’s age and financial satisfaction their life satisfaction?

• The outcome/DV (\(Y\)): life_satisfaction
• The predictors/IV (\(X\)): financial_satisfaction and age

life_model2 <- lm(life_satisfaction ~ financial_satisfaction + age, 
                  data = wvs_cleaned)
summary(life_model2)

Linear Regression: Multiple continuous predictors

Call:
lm(formula = life_satisfaction ~ financial_satisfaction + age, 
    data = wvs_cleaned)

Residuals:
    Min      1Q  Median      3Q     Max 
-8.0571 -0.7459  0.1272  0.7919  5.8965 

Coefficients:
                       Estimate Std. Error t value Pr(>|t|)    
(Intercept)            3.346623   0.069441  48.194  < 2e-16 ***
financial_satisfaction 0.529454   0.008084  65.494  < 2e-16 ***
age                    0.005546   0.001046   5.305 1.17e-07 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.382 on 6400 degrees of freedom
Multiple R-squared:  0.4148,    Adjusted R-squared:  0.4146 
F-statistic:  2268 on 2 and 6400 DF,  p-value: < 2.2e-16

Possible way to explain the result

A multiple regression analysis was conducted to examine how financial satisfaction and age predict life satisfaction. Financial satisfaction was a strong predictor (B = 0.529, SE = 0.008, p < 0.001), indicating that for each one-unit increase in financial satisfaction, life satisfaction increased by 0.529 units. Age was also a significant but weaker predictor (B = 0.006, SE = 0.001, p < 0.001), with each additional year of age associated with a 0.006-unit increase in life satisfaction.

The model was statistically significant (F(2, 6400) = 2268, p < 0.001) and explained 41.5% of the variance in life satisfaction (R² = 0.415, Adjusted R² = 0.415).

Present your regression result - tbl_regression() from gtsummary

life_model2 |> tbl_regression() |> bold_p()

Characteristic	Beta	95% CI1	p-value
financial_satisfaction	0.53	0.51, 0.55	<0.001
age	0.01	0.00, 0.01	<0.001
1 CI = Confidence Interval

More on tbl_regression() by gtsummary: https://www.danieldsjoberg.com/gtsummary/reference/tbl_regression.html

Reporting result: A sample regression table

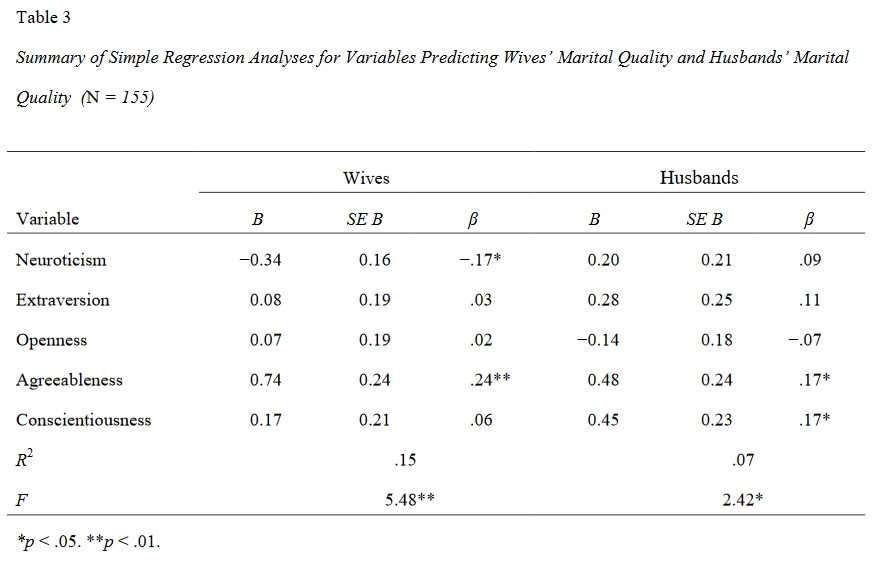
You might encounter different table formats when reporting regression results, but there are some key elements that should generally be included.

These are: the number of observations (\(N\)), the coefficients (B = unstandardized, raw coeff in original unit of measurements; \(\beta\) = standardized, converted to standard deviation units), standard errors (SE), confidence intervals (95% CI), and p-values. Other metrics to include are the \(R^2\) and \(F\) statistics.

• The above screenshot is taken from https://www.ncfr.org/system/files/2017-01/regression_0.pdf
• APA recommended format

Presenting your models

If you get an error saying “huxreg not found”, you may need to:

1. Install the library by running this line in your terminal: install.packages("huxtable")

2. And then load them to your script with this line: library(huxtable)

For more info about huxreg, go here: https://cran.r-project.org/web/packages/huxtable/vignettes/huxreg.html

huxreg("life_satisfaction (model1)" = life_model1, 
       "life_satisfaction (model2)" = life_model2,
       number_format = 4,
       bold_signif = 0.05,
       statistics = c( "R squared" = "r.squared", "N" = "nobs", "F" = "statistic",
      "P value" = "p.value"))

Presenting your models

	life_satisfaction (model1)	life_satisfaction (model2)
(Intercept)	6.3264 ***	3.3466 ***
	(0.0678)	(0.0694)
age	0.0162 ***	0.0055 ***
	(0.0013)	(0.0010)
financial_satisfaction		0.5295 ***
		(0.0081)
R squared	0.0225	0.4148
N	6403	6403
F	147.6646	2268.0004
P value	0.0000	0.0000
*** p < 0.001; ** p < 0.01; * p < 0.05.

FYI: Multicollinearity

Caution! When doing regression-type of tests, watch out for multicollinearity.

Multicollinearity is a situation in which two or more predictor variables are highly correlated with each other. This makes it difficult to determine the specific contribution of each predictor variable to the relationship.

One way to check for it:

• Assess the correlation between your predictor variables in your model using Variance Inflation Factor (VIF)

• If they seem to be highly correlated (> 5 or so), one of the easiest (and somewhat acceptable) way is to simply remove the less significant predictor from your model :D

car::vif(life_model2)

financial_satisfaction                    age 
              1.024893               1.024893 

Linear Regression: One categorical predictor

Research Question: Explore the difference in life satisfaction between age groups

• The outcome/DV (\(Y\)): life_satisfaction
• The predictor/IV (\(X\)): age_group

Note

Before proceeding with analysis, ensure that all the categorical variables involved are cast as factors!

str(wvs_cleaned$life_satisfaction)

 num [1:6403] 7 5 8 6 6 8 9 8 8 10 ...

str(wvs_cleaned$age_group)

 Factor w/ 4 levels "61+","45-60",..: 1 1 1 1 1 1 1 1 1 1 ...

Continuing the analysis

The analysis summary should look like this:

life_model3 <- lm(life_satisfaction ~ age_group, data = wvs_cleaned)
summary(life_model3)

Call:
lm(formula = life_satisfaction ~ age_group, data = wvs_cleaned)

Residuals:
    Min      1Q  Median      3Q     Max 
-6.5293 -1.0131  0.3391  0.9869  3.3391 

Coefficients:
               Estimate Std. Error t value Pr(>|t|)    
(Intercept)     7.52931    0.04296 175.250   <2e-16 ***
age_group45-60 -0.51622    0.05984  -8.626   <2e-16 ***
age_group29-44 -0.49386    0.05961  -8.284   <2e-16 ***
age_group18-28 -0.86840    0.07124 -12.190   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.783 on 6399 degrees of freedom
Multiple R-squared:  0.02533,   Adjusted R-squared:  0.02488 
F-statistic: 55.44 on 3 and 6399 DF,  p-value: < 2.2e-16

• When interpreting a categorical predictor in regression, one category is treated as the reference category, which serves as the baseline for comparison. In this case, the reference category corresponds to the intercept.

• By default, the first category in the data is used as the reference category, unless specified.

Narrating the result

Here is one possible way to narrate your result:

A linear regression analysis was conducted to examine how age groups predict life satisfaction. With the youngest age group (15-28) as the reference group (intercept = 6.66, SE = 0.06), all other age groups showed significantly higher life satisfaction. The 29-44 age group scored 0.37 units higher (SE = 0.07, p < 0.001), the 45-60 age group scored 0.35 units higher (SE = 0.07, p < 0.001), and the 61+ age group showed the largest difference, scoring 0.87 units higher (SE = 0.07, p < 0.001) than the reference group.

The model was statistically significant (F(3, 6399) = 55.44, p < 0.001) but only explained 2.5% of the variance in life satisfaction (R² = 0.025, Adjusted R² = 0.025).

Presenting the regression table

huxreg("life satisfaction (model3)" = life_model3,
       number_format = 4,
       bold_signif = 0.05,
       statistics = c( "R squared" = "r.squared", "N" = "nobs", "F" = "statistic",
      "P value" = "p.value"))

Presenting the regression table

	life satisfaction (model3)
(Intercept)	7.5293 ***
	(0.0430)
age_group45-60	-0.5162 ***
	(0.0598)
age_group29-44	-0.4939 ***
	(0.0596)
age_group18-28	-0.8684 ***
	(0.0712)
R squared	0.0253
N	6403
F	55.4384
P value	0.0000
*** p < 0.001; ** p < 0.01; * p < 0.05.

Categorical predictor: changing the reference

Let’s change the reference category for age_group variable to “61+”.

wvs_cleaned <- wvs_cleaned |> 
    mutate(age_group = relevel(age_group, ref = "61+"))

str(wvs_cleaned$age_group)

 Factor w/ 4 levels "61+","45-60",..: 1 1 1 1 1 1 1 1 1 1 ...

Re-run the analysis with the new reference category

life_model3a<- lm(life_satisfaction ~ age_group, data = wvs_cleaned)
summary(life_model3a)

Categorical predictor: changing the reference

Call:
lm(formula = life_satisfaction ~ age_group, data = wvs_cleaned)

Residuals:
    Min      1Q  Median      3Q     Max 
-6.5293 -1.0131  0.3391  0.9869  3.3391 

Coefficients:
               Estimate Std. Error t value Pr(>|t|)    
(Intercept)     7.52931    0.04296 175.250   <2e-16 ***
age_group45-60 -0.51622    0.05984  -8.626   <2e-16 ***
age_group29-44 -0.49386    0.05961  -8.284   <2e-16 ***
age_group18-28 -0.86840    0.07124 -12.190   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.783 on 6399 degrees of freedom
Multiple R-squared:  0.02533,   Adjusted R-squared:  0.02488 
F-statistic: 55.44 on 3 and 6399 DF,  p-value: < 2.2e-16

Changing baseline category for ordered factor

Assuming we have a column with ordered factor in our data called education with the level of Primary, Secondary, and Tertiary. This is how we can change the order, if we want to put Secondary before Primary.

wvs_cleaned <- wvs_cleaned |> 
    mutate(education = factor(education, 
                         levels = c("Secondary", "Primary", "Tertiary"), 
                         ordered = TRUE))

Releveling ordered factor

Previously, we could use the relevel() function to change the reference category for ordered factors. However, in recent R versions, this no longer works for ordered factors, so we now use the method shown in the code above. The relevel() function still works for unordered factors.

Let’s try this Linear Regression exercise! (5 mins)

Create a regression model called life_model4 that predicts the life_satisfaction score based on sex. The reference category should be ‘Male’

life_model4 <- lm(life_satisfaction ~ sex, data = wvs_cleaned)
summary(life_model4)

Call:
lm(formula = life_satisfaction ~ sex, data = wvs_cleaned)

Residuals:
    Min      1Q  Median      3Q     Max 
-6.1136 -1.0949 -0.0949  0.9051  2.9051 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  7.09492    0.03207 221.211   <2e-16 ***
sexFemale    0.01863    0.04514   0.413     0.68    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.806 on 6401 degrees of freedom
Multiple R-squared:  2.66e-05,  Adjusted R-squared:  -0.0001296 
F-statistic: 0.1703 on 1 and 6401 DF,  p-value: 0.6799

Binary Logistic Regression

Binary Logistic Regression - what is it?

Also known as simply logistic regression, it is used to model the relationship between a set of independent variables and a binary outcome.

These independent variables can be either categorical or continuous.

Binary Logistics Regression formula:

\[ logit(P) = \beta_0 + \beta_1X_1 + \beta_2X_2 + … + \beta_nX_n \]

It can also be written like below, in which the \(logit(P)\) part is expanded:

\[ P = \frac{1}{1 + e^{-(\beta_0 + \beta_1X)}} \]

Binary Logistic Regression Examples

• Does a person’s age and education level influence whether they will vote Democrat or Republican in the US election?
• Does the number of hours spent studying impact a student’s likelihood of passing a module? (pass/fail outcome)

In essence, the goal of binary logistic regression is to estimate the probability of a specific event happening when there are only two possible outcomes (hence the term “binary”).

Binary Logistic Regression: One Continuous Predictor

Research Question: Does a participant’s political alignment affect the likelihood of being satisfied with life?

• The outcome/DV (\(Y\)): satisfied

  • Our outcome is a continuous variable, but for the purpose of this workshop practice, let’s define the outcome as “Satisfied” if the life_satisfaction score is more than 7 (inclusive), and “not Satisfied” if the score is less than 7.

• The predictor/IV (\(X\)): political_scale

Dummy-coding dependent variable

Before we proceed with the calculations, we need to dummy code the dependent variable into 1 and 0, with 1 = Satisfied and 0 = Not Satisfied. More info on dummy coding here

# First, we need to create a binary outcome
wvs_cleaned <- wvs_cleaned |>
    mutate(satisfied = if_else(life_satisfaction >= 7, 1, 0))
# the if_else is from dplyr package (from session 2)

# A tibble: 6,403 × 2
  life_satisfaction satisfied
              <dbl>     <dbl>
1                 7         1
2                 5         0
3                 8         1
4                 6         0
5                 6         0
# ℹ 6,398 more rows

Conduct the analysis

Let’s conduct the analysis!

life_model5 <- glm(satisfied ~ political_scale,
                family = binomial, 
                data = wvs_cleaned)

summary(life_model5)

Call:
glm(formula = satisfied ~ political_scale, family = binomial, 
    data = wvs_cleaned)

Coefficients:
                Estimate Std. Error z value Pr(>|z|)    
(Intercept)      0.45438    0.07236   6.279 3.41e-10 ***
political_scale  0.08448    0.01326   6.370 1.89e-10 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 7731  on 6402  degrees of freedom
Residual deviance: 7690  on 6401  degrees of freedom
AIC: 7694

Number of Fisher Scoring iterations: 4

Exponentiate the coefficients

If you recall the formula, the results are expressed in Logit Probability. As we typically report the result in terms of Odd Ratios (OR), perform exponentiation on the coefficients.

exp(coef(life_model5))

    (Intercept) political_scale 
       1.575194        1.088155 

We can also use tbl_regression() to do this for us:

library(gtsummary)
life_model5 |> tbl_regression(exponentiate = TRUE) |> 
    bold_p() 

Characteristic	OR1	95% CI1	p-value
political_scale	1.09	1.06, 1.12	<0.001
1 OR = Odds Ratio, CI = Confidence Interval

More on tbl_regression() by gtsummary: https://www.danieldsjoberg.com/gtsummary/reference/tbl_regression.html

Get the χ² (chi-squared) to report model significance

χ² (Chi-squared) goodness of fit tests whether your model fits the data significantly better than a null model (model with no predictors). As you can see, it is not in the glm() result, but we can calculate this somewhat manually using the Null and Residual deviance and df like so:

• Null deviance: 7731
• Residual deviance: 7690
• Difference: 7731 - 7690 = 41 (this is the χ² value)

To get the p-value, we need the degree of freedom and the χ²:

• df = difference in degrees of freedom (6402 - 6401 = 1)
• χ² = 41

pchisq(41, df=1, lower.tail=FALSE)  # will give p-value

[1] 1.522292e-10

Get the χ² (chi-squared) and Pseudo R-squared (for reporting purposes)

In the report, the model’s χ² (chi-squared) and R-squared (indicating the proportion of variance that can be explained by the model) should be included. However, since the resulting item does not have this info, we will call upon DescTools’ PseudoR2() function to help!

# by default, McFadden will be used
DescTools::PseudoR2(life_model5) 

   McFadden 
0.005306369 

We can retrieve the R-squared value and the χ² (also known as the G2 value, which stands for Goodness-of-fit) at the same time like so:

DescTools::PseudoR2(life_model5, 
                    which = c("G2", "Nagelkerke"))

          G2   Nagelkerke 
41.023494851  0.009110118 

In case you need to get other Rsquared methods

DescTools::PseudoR2(life_model5, 
                    which = "all")

       McFadden     McFaddenAdj        CoxSnell      Nagelkerke   AldrichNelson 
   5.306369e-03    4.788971e-03    6.386437e-03    9.110118e-03    6.366131e-03 
VeallZimmermann           Efron McKelveyZavoina            Tjur             AIC 
   1.163872e-02    5.980444e-03    9.450630e-03    6.188032e-03    7.693968e+03 
            BIC          logLik         logLik0              G2 
   7.707497e+03   -3.844984e+03   -3.865496e+03    4.102349e+01 

Possible interpretation of the result

Possible interpretation:

(The intercept isn’t typically interpreted as an odds ratio, so we’ll ignore that for now)

A logistic regression was performed to ascertain the effects of political scale alignment on the likelihood that individuals will be satisfied with life versus not satisfied. The logistic regression model was statistically significant, χ² (1, N = 6403) = 41.02, p < .001.

The model explained 0.9% (Nagelkerke R²) of the variance in life satisfaction. Political scale alignment was associated with an increased likelihood of being satisfied with life (OR = 1.09, 95% CI [1.06, 1.12], p < .001), indicating that for each one-unit increase in political scale alignment (1-10), the odds of being satisfied with life increased by 9%.

More on interpreting Odds Ratio: https://stats.oarc.ucla.edu/other/mult-pkg/faq/general/faq-how-do-i-interpret-odds-ratios-in-logistic-regression/

Recap - why do I need to report these?

• χ² (Chi-squared) goodness of fit tests whether your model fits the data significantly better than a null model (model with no predictors).

• “Standard” R-squared isn’t typically reported for logistic regression because it’s not as meaningful as it is in linear regression. But we do still want to see how much of the variance in the data can be explained by the model.

• Pseudo R-squared tries to mimic traditional R-squared by showing how much of the variation in the outcome your model explains, but it’s adjusted to work with binary outcomes. It’s sort of answering the question of “How well does my model explain the data?”

• It is possible to have a significant χ² (meaning your model is statistically significant and better than nothing) but a low Pseudo R-squared (showing it still doesn’t explain much variation). This isn’t contradictory - it just means your model is better than random guessing but there’s still a lot of unexplained variation. (Pretty common in social sciences; after all, human behaviours are complex!)

FYI - IRL sample of reporting Logistic Regression

Below is a sample of how you may want to narrate your result. Note the resulting values mentioned in the paragraph below.

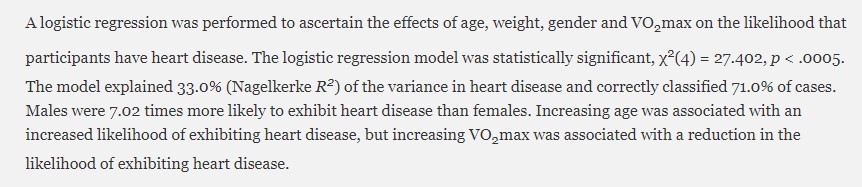
In a nutshell, you will most likely have to mention the p-value, the coefficients (for linear regressions), the Odd Ratios (for logistic regression) with the confidence intervals, the chi-squared (χ²), and the R-squared. You should also include these information in your regression table.

The screenshot is retrieved from https://statistics.laerd.com/spss-tutorials/binomial-logistic-regression-using-spss-statistics.php

Regression tables

Even with huxtable, you may need to edit the table further to include the missing stats

huxreg("life_satisfaction" = life_model5, statistics = c("R2" = "r.squared", "logLik", "AIC"))

	life_satisfaction
(Intercept)	0.454 ***
	(0.072)
political_scale	0.084 ***
	(0.013)
logLik	-3844.984
AIC	7693.968
*** p < 0.001; ** p < 0.01; * p < 0.05.

Binary Logistic Regression: One Categorical Predictor

Research Question: Does religiousity affect the likelihood of being satisfied with life?

• The outcome/DV (\(Y\)): satisfied
• The predictor/IV (\(X\)): religiousity - let’s set “A religious person” as the reference category!

wvs_cleaned <- wvs_cleaned |> 
    mutate(religiousity = relevel(religiousity, ref = "A religious person"))

life_model6 <- glm(satisfied ~ religiousity,
                      family = "binomial",
                      data = wvs_cleaned)

summary(life_model6)

Binary Logistic Regression: One Categorical Predictor

Call:
glm(formula = satisfied ~ religiousity, family = "binomial", 
    data = wvs_cleaned)

Coefficients:
                                   Estimate Std. Error z value Pr(>|z|)    
(Intercept)                         1.00703    0.04426  22.753  < 2e-16 ***
religiousityNot a religious person -0.17379    0.06111  -2.844 0.004456 ** 
religiousityAn atheist             -0.27498    0.07845  -3.505 0.000456 ***
religiousityDon't know              0.21675    0.36245   0.598 0.549832    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 7731.0  on 6402  degrees of freedom
Residual deviance: 7715.3  on 6399  degrees of freedom
AIC: 7723.3

Number of Fisher Scoring iterations: 4

exp(coef(life_model6))

                       (Intercept) religiousityNot a religious person 
                         2.7374462                          0.8404704 
            religiousityAn atheist             religiousityDon't know 
                         0.7595839                          1.2420335 

Exponentiate the coefficients

If you recall the formula, the results are expressed in Logit Probability. As we typically report the result in terms of Odd Ratios (OR), perform exponentiation on the coefficients.

library(gtsummary)
life_model6 |> tbl_regression(exponentiate = TRUE) |>  
    bold_p()

Characteristic	OR1	95% CI1	p-value
religiousity
A religious person	—	—
Not a religious person	0.84	0.75, 0.95	0.004
An atheist	0.76	0.65, 0.89	<0.001
Don't know	1.24	0.63, 2.67	0.5
1 OR = Odds Ratio, CI = Confidence Interval

Get the Rsquared

Let’s retrieve the R-squared value and the Chi-square χ² value (also known as the G2 value, which stands for Goodness-of-fit)

DescTools::PseudoR2(life_model6, 
                    which = c("G2", "Nagelkerke"))

          G2   Nagelkerke 
15.652088008  0.003482759 

# get the other R-squared if you like
DescTools::PseudoR2(life_model6, 
                    which = "all")

       McFadden     McFaddenAdj        CoxSnell      Nagelkerke   AldrichNelson 
   2.024590e-03    9.897938e-04    2.441508e-03    3.482759e-03    2.438532e-03 
VeallZimmermann           Efron McKelveyZavoina            Tjur             AIC 
   4.458185e-03    2.438152e-03    3.608656e-03    2.438152e-03    7.723340e+03 
            BIC          logLik         logLik0              G2 
   7.750398e+03   -3.857670e+03   -3.865496e+03    1.565209e+01 

Narrating the results

Possible interpretation:

(The intercept isn’t typically interpreted as an odds ratio, so we’ll ignore that for now)

A logistic regression was performed to ascertain the effects of religiosity on the likelihood that individuals will be satisfied with life versus not satisfied. The logistic regression model was statistically significant, χ² (3, N = 6403) = 15.65, p < .001.

The model explained 0.3% (Nagelkerke R²) of the variance in life satisfaction. Compared to religious persons (reference group), being non-religious was associated with lower odds of life satisfaction (OR = 0.84, 95% CI [0.74, 0.95], p = .004), and being an atheist was also associated with lower odds of life satisfaction (OR = 0.76, 95% CI [0.65, 0.89], p < .001). There was no significant difference in life satisfaction for those who were unsure about their religious beliefs compared to religious persons (OR = 1.24, 95% CI [0.61, 2.52], p = .550).

More on logistic regression: https://stats.oarc.ucla.edu/r/dae/logit-regression/

Present both models in a table

Note that the R-squared is missing here, so be sure to put that in when you paste this table to your document.

library(huxtable)
huxreg(life_model5, life_model6)

	(1)	(2)
(Intercept)	0.454 ***	1.007 ***
	(0.072)	(0.044)
political_scale	0.084 ***
	(0.013)
religiousityNot a religious person		-0.174 **
		(0.061)
religiousityAn atheist		-0.275 ***
		(0.078)
religiousityDon't know		0.217
		(0.362)
N	6403	6403
logLik	-3844.984	-3857.670
AIC	7693.968	7723.340
*** p < 0.001; ** p < 0.01; * p < 0.05.

Let’s try this Logistic Regression exercise! (5 mins)

Create a regression model called life_model7 that predicts the likelihood of being satisfied with life based on sex.

life_model7 <- glm(satisfied ~ sex,
                  family = "binomial", 
                  data = wvs_cleaned) 

summary(life_model7)
exp(coefficients(life_model7))

What is Quarto? What is Markdown?

Markdown (Specifically, R Markdown)

• Markdown is a lightweight markup language that provides a simple and readable way to write formatted text without using complex HTML or LaTeX. It is designed to make authoring content easy for everyone!

  • Markdown files can be converted into HTML or other formats.
  • Generic Markdown file will have .md extension.

• R Markdown is an extension of Markdown that incorporates R code chunks and allows you to create dynamic documents that integrate text, code, and output (such as tables and plots).

  • RMarkdown file will have .Rmd extension.

RMarkdown in action

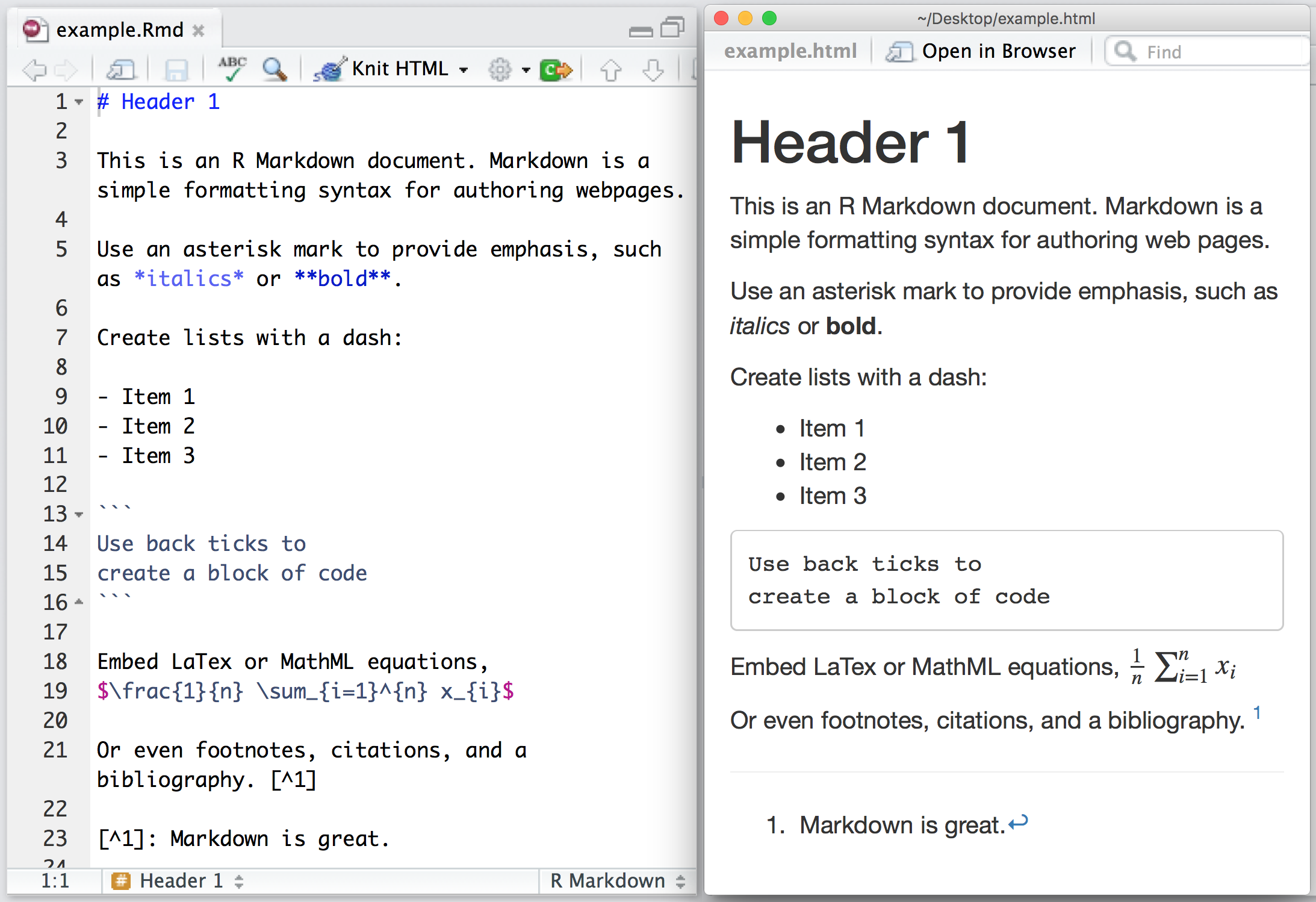
How it all works

Illustration by Allison Horst (www.allisonhorst.com)

Quarto

• Quarto is a multi-language, next-generation version of R Markdown from Posit and includes dozens of new features and capabilities while at the same being able to render most existing Rmd files without modification.

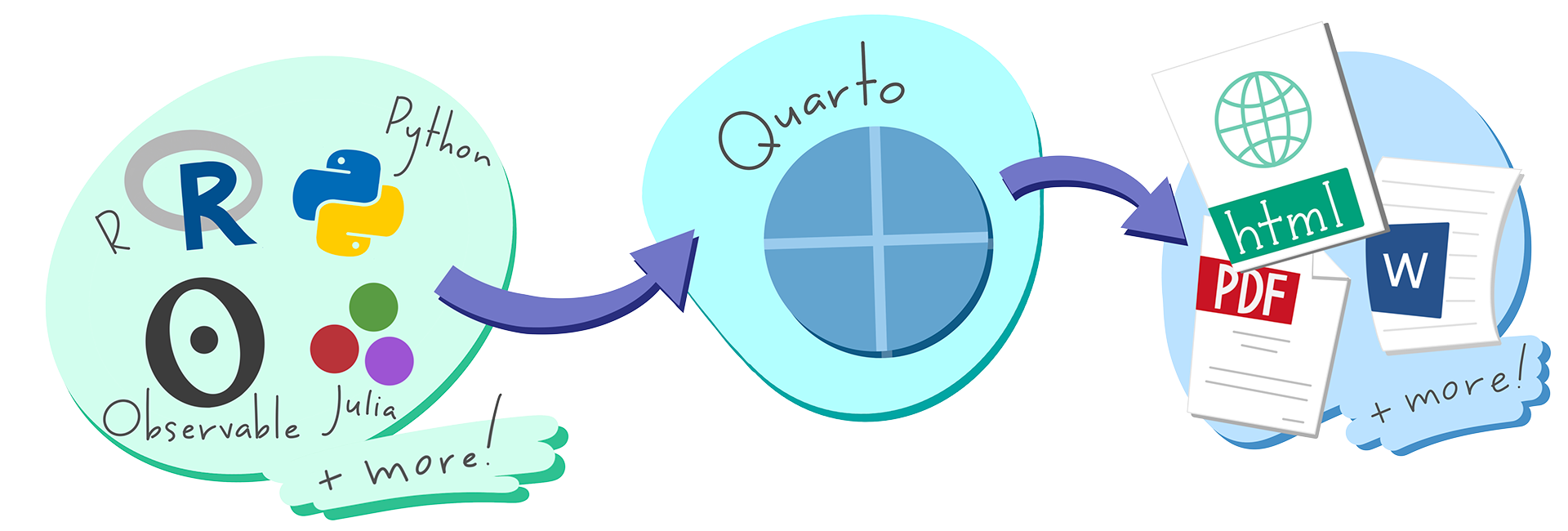
Illustration by Allison Horst (www.allisonhorst.com)

Quarto in action: R scripts + Markdown

R Scripts vs Quarto

R Scripts

• Great for quick debugging, experiment

• Preferred format if you are archiving your code to GitHub or data repository

• More suitable for “production” tasks e.g. automating your data cleaning and processing, custom functions, etc.

Quarto

• Great for report and presentation to showcase your research insights/process as it integrates code, narrative text, visualizations, and results.

• Very handy when you need your report in multiple format, e.g. in Word and PPT.

• Fun fact: the course website and slides are all made in Quarto

If you are interested to learn more about this…

SMU Libraries regularly host Quarto workshops every semester from week 2 to week 6, taught by Prof Kam Tin Seong.

Keep a lookout for these titles:

• R Ep.1: Making Your Research Reproducible with Quarto in RStudio
• R Ep.7: Creating Awesome Web Slides in Quarto with Revealjs
• R Ep.9: Building Website and Blog with Quarto

Best Practices + More Resources

R Best Practices

• Use <- for assigning values to objects.

  • Only use = when passing values to a function parameter.

• Do not alter your raw data; save your wrangled/cleaned data into a new file and keep it separate from the raw data.

• Make use of R projects to organize your data and make it easier to send over to your collaborators.

  • Having said that, when it comes to coding project, the best way to collaborate is using GitHub or similar platforms.

• Whenever possible and makes sense for your project, follow the common convention when naming your objects, scripts, and functions. One guide that you can follow is Hadley Wickham’s tidyverse style guide.

References for APA Guidelines on Reporting statistics

Do check with your professor on how closely you should follow the guidelines, or if there is any specific format required.

• APA Style 7th Edition Numbers and Statistics Guide
• University of Washington - Reporting Results of Common Statistical Tests in APA Format
• Illinois State University - A Short Guide to Handling Numbers and Statistics in APA Format (in 6th Edition)
• Statistic Tables in APA recommended format

Thank you for your participation 😄

All the best for your studies and academic journey! (manifesting excellent grades for everyone who attended the workshop)

Need help with R or Quarto? Please don’t hesitate to contact me at bellar@smu.edu.sg

Post-workshop survey

Please scan this QR code or click on the link below to fill in the post-workshop survey. It should not take more than 2-3 minutes.

Survey link: https://smusg.asia.qualtrics.com/jfe/form/SV_ai0mSfHjwWZWC2y