Data Visualization and Descriptive Stats

Bella Ratmelia

Today’s Outline

1. Univariate descriptive stats and visualization
   • for continuous variable
   • for categorical variable (frequency or proportion)
2. Bivariate (two variables) descriptive stats and visualization
   • both categorical
   • both continuous (+ correlation plot)
   • one categorical, one continuous
3. Using Facets
4. Best practices
5. Recap + Quiz!

Checklist when you start RStudio

• Load the project we created last session and open the R script file.
• Make sure that Environment panel is empty (click on broom icon to clean it up)
• Clear the Console and Plots too.
• Re-run the library(tidyverse) and read_csv portion in the previous session

Refresher: Loading from CSV into a dataframe

Use read_csv from readr package (part of tidyverse) to load our data into a dataframe

# import tidyverse library
library(tidyverse)

# read the CSV with WVS data
wvs_cleaned <- read_csv("data-output/wvs_cleaned_v1.csv")

# Convert categorical variables to factors
columns_to_convert <- c("country", "religiousity", "sex", "marital_status", "employment")

wvs_cleaned <- wvs_cleaned |> 
    mutate(across(all_of(columns_to_convert), as_factor))

# peek at the data, pay attention to the data types!
glimpse(wvs_cleaned)

Recap: Descriptive Statistics

• Univariate (i.e. single variable) Descriptive Stats

  • Measures of central tendency: mean(), median(), Mode()
  • Measures of Variability: min(), max(), range(), IQR(), sd() (standard deviation), var() (variance)
  • Distribution shape: skewness() and kurtosis() from moments library. This is easier to see with histogram

• Bivariate (i.e. two variables) Descriptive Stats

  • Contingency table / cross tab (for categorical data)
  • Covariance - describe how two variables vary together
  • Correlation - describe relationship strength and direction in a sample. (If we want to use this to infer about a population from a sample, it would fall under inferential stats)
  • Visualizations e.g. Scatterplots, side-by-side boxplots, stacked bar charts, etc.

Recap: Basic R Functions for Descriptive Stats

Last week, we explored some basic R functions for descriptive statistics.

• mean(): arithmetic average
• median(): middle value
• sd(): standard deviation
• var(): variance
• range(): range of values
• IQR(): interquartile range
• summary(): provides a summary of descriptive statistics
• Mode() function from DescTools package: the most frequently occuring value ¹

1. R doesn’t have built-in functions for mode, so we need DescTools package to get this function

Recap: Long vs Wide Data

Long data:

• Each row is a unique observation.

• There is a separate column indicating the variable or type of measurements

• This format is more “understandable” by R, more suitable for visualizations (which we’ll explore more next week!)

Wide data:

• Each row is a value in variables.

• Each column is a value in variables –> the more values you have, the “wider” is the data

• This format is more intuitive for humans!

Long vs Wide Data: Examples

Long data:

Observations (Long)

country	age_group	count
CAN	18-28	712
CAN	29-44	1232
CAN	45-60	1061
CAN	61+	1013
NZL	18-28	27
NZL	29-44	119
NZL	45-60	222
NZL	61+	292
SGP	18-28	246
SGP	29-44	511
SGP	45-60	550
SGP	61+	418

Wide data:

Observations (Wide)

country	18-28	29-44	45-60	61+
CAN	712	1232	1061	1013
NZL	27	119	222	292
SGP	246	511	550	418

Long vs Wide Data: One way to spot

Pay attention to the columns of the data.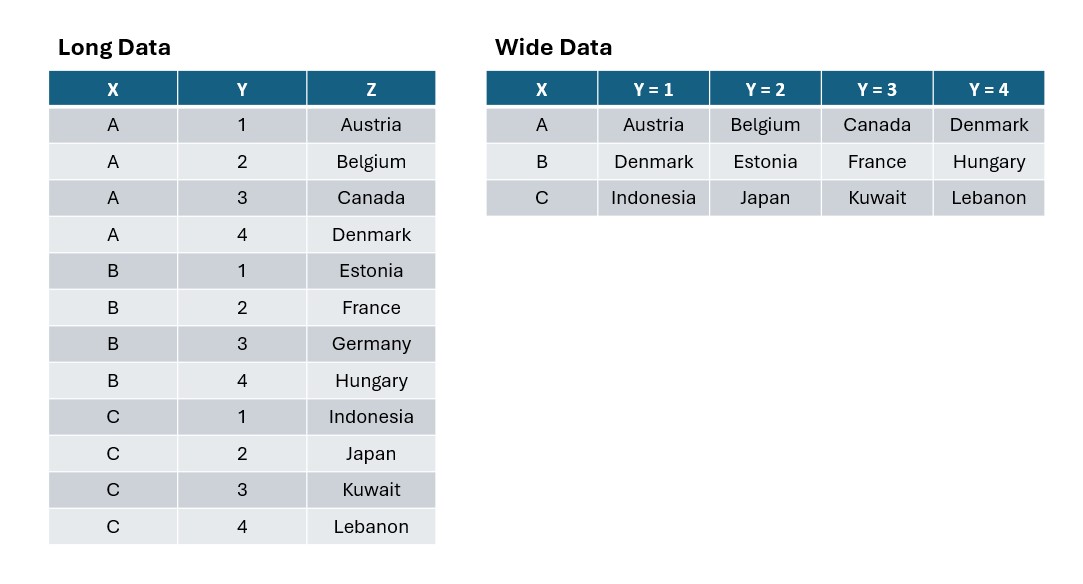

Univariate Descriptive Stats + Visualization

Measures of Central Tendency

Let’s start by examining the age variable in our dataset.

library(DescTools)
# if you get an error, install the library first with this code:
# install.packages("DescTools")

# Basic statistics
mean_age <- mean(wvs_cleaned$age, na.rm = TRUE)
median_age <- median(wvs_cleaned$age, na.rm = TRUE)
mode_age <- DescTools::Mode(wvs_cleaned$age, na.rm = TRUE)

# Print results
cat("Mean age:", mean_age, "\n") # cat stands for concatenate

Mean age: 47.96408 

cat("Median age:", median_age, "\n")

Median age: 48 

cat("Most frequently occuring age:", mode_age, "\n") # this is here just for demo purposes

Most frequently occuring age: 54 

How we can interpret / report this:

“The age distribution of this sample is fairly symmetrical, as indicated by the very close mean (48 years) and median (48 years) values. The mode of 54 years suggests a slight right-skew in the age distribution, with a cluster of participants in their mid-50s.”

Measures of Variability or Dispersion

var_age <- var(wvs_cleaned$age, na.rm = TRUE)
sd_age <- sd(wvs_cleaned$age, na.rm = TRUE)
range_age <- range(wvs_cleaned$age, na.rm = TRUE)
iqr_age <- IQR(wvs_cleaned$age, na.rm = TRUE)

cat("Variance of age:", var_age, "\n")

Variance of age: 279.6066 

cat("Standard deviation of age:", sd_age, "\n")

Standard deviation of age: 16.72144 

cat("Range of age:", range_age[1], "to", range_age[2], "\n")

Range of age: 18 to 93 

cat("Interquartile range of age:", iqr_age, "\n")

Interquartile range of age: 28 

How we can interpret / report this:

“The age distribution of this sample is fairly wide spread. With a standard deviation of 16.72144, suggesting that most individuals’ ages deviate from the mean by approximately 16.72 years. The range of ages spans from 18 to 93 years, which covers a wide range of age groups within the sample. The interquartile range (IQR) of 28 years, which represents the middle 50% of the data, indicates a moderately wide distribution of ages in the central portion of the dataset.”

Distribution Shape

The function skewness() and kurtosis() is available through R package called moments. You may need to install it first before calling the library and its functions like in this code below.

library(moments)
# if you get an error, install the library first with this code:
# install.packages("moments")

skew_age <- skewness(wvs_cleaned$age, na.rm = TRUE)
kurtosis_age <- kurtosis(wvs_cleaned$age, na.rm = TRUE)

cat("Skewness of age:", skew_age, "\n")

Skewness of age: 0.1009475 

cat("Kurtosis of age:", kurtosis_age, "\n")

Kurtosis of age: 2.018238 

How we can interpret / report this:

“The age distribution has a very slight right skew (skewness = 0.10), meaning there are slightly more outliers toward older ages, but the skew is minimal since values between -0.5 and 0.5 are considered approximately symmetric. The kurtosis of 2.02 is lower than a normal distribution’s kurtosis of 3, indicating this distribution is platykurtic - it has lighter tails and is more uniform or”flatter” than a normal distribution.”

Visualizing with ggplot - Histogram

• Describing the spread and shape of distribution with just words is not very productive, so typically it is accompanied with visualization.

• ggplot is plotting package that is included inside tidyverse package

• works best with data in the long format, i.e., a column for all the dimensions/measures and another column for the value for each dimension/measure.

wvs_cleaned |> 
    ggplot(aes(x = age)) +
    geom_histogram(binwidth = 1, fill = "lightblue", color = "navy") +
    labs(title = "Age distribution of respondents",
         x = "Age",
         y = "Count") +
    theme_minimal()

Visualizing with ggplot - Histogram

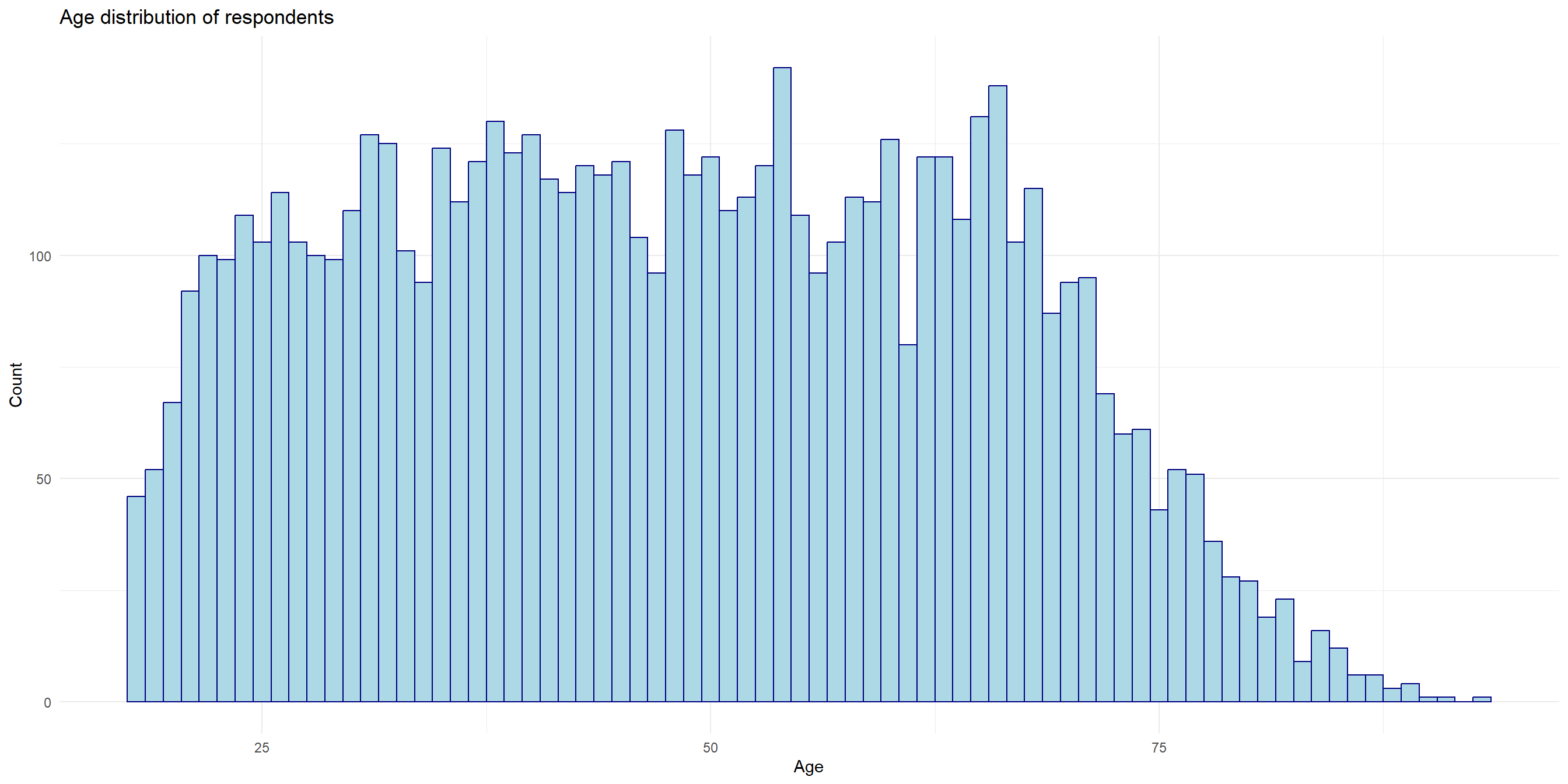
Anatomy of ggplot code

Charts built with ggplot must include the following:

1wvs_cleaned |>
2    ggplot(aes(x = age)) +
3    geom_histogram(binwidth = 1, fill = "lightblue", color = "navy") +
4    labs(title = "Age distribution of respondents",
         x = "Age",
         y = "Count") +
5    theme_minimal()

1

Data - the dataframe/tibble to visualize.

2

Aesthetic mappings (aes) - describes which variables are mapped to the x, y axes, alpha (transparency) and other visual aesthetics.

3

Geometric objects (geom) - describes how values are rendered; as bars, scatterplot, lines, etc.

4

Provide titles and labels to your graph

5

(Optional) apply a theme/look to your graph

Tip: open the ggplot cheatsheet

Tip

A strategy I’d like to recommend: briefly read over the ggplot2 documentation and have them open on a separate tab. Figure out the type of variables you need to visualize (discrete or continuous) to quickly identify which visualization would make sense.

ggplot documentation link

Continuous Data - Boxplot

Let’s visualize the variability with boxplot to get a better sense of the spread.

wvs_cleaned |> 
    ggplot(aes(x = age)) +
    geom_boxplot(fill = "lightblue", color = "navy") +
    labs(title = "Age distribution of respondents",
         x = "Age") +
    theme_minimal()

Continuous Data - Boxplot

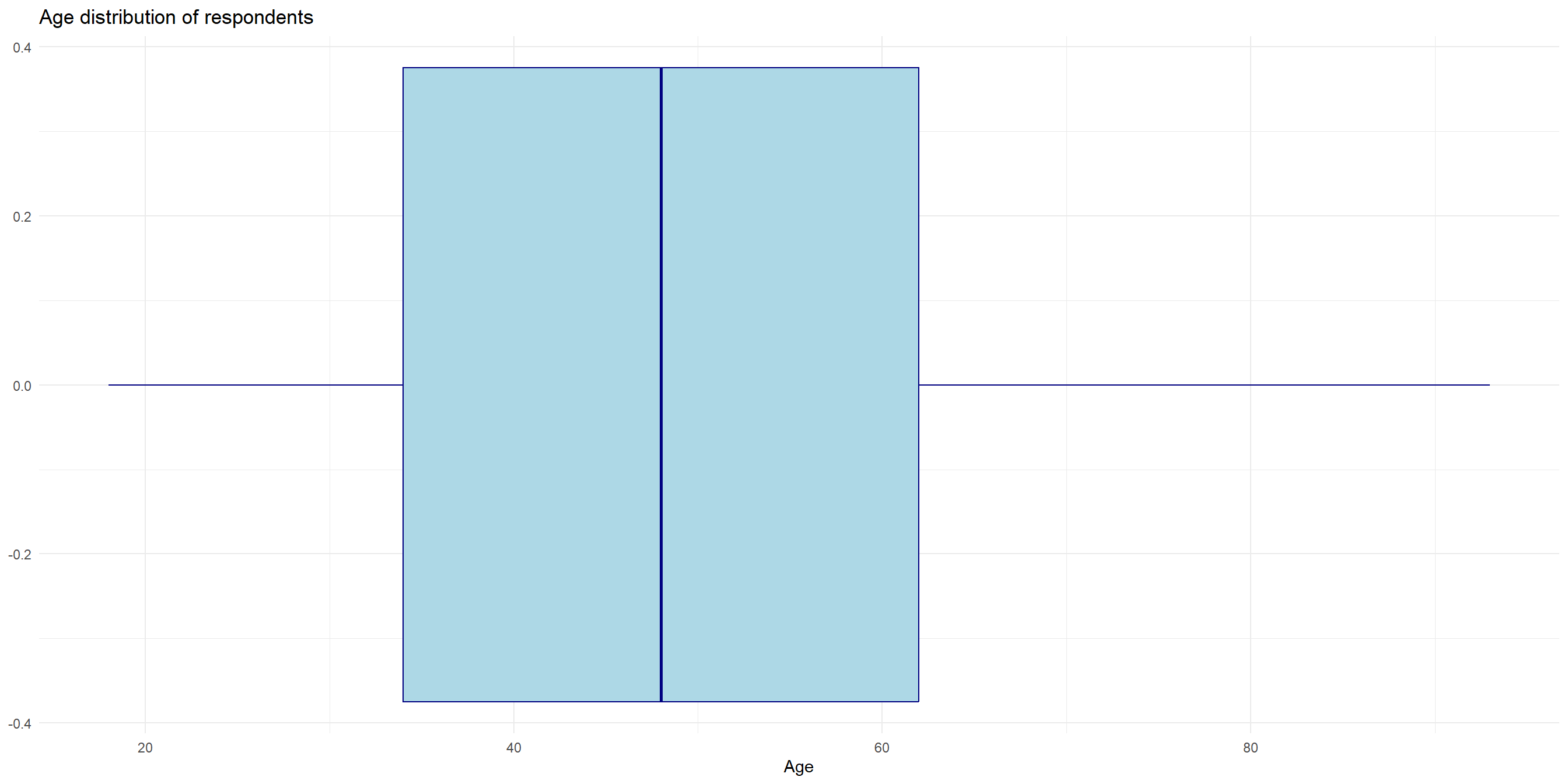
Categorical Data - Bar chart for frequency distribution

• The age variable is a numerical / continuous data. We can’t apply mean(), median() and other central tendency measures to categorical data such as age_group or employment_status. We can, however, visualize them.

• When dealing with categorical data, first take note on whether you want to visualize the proportion or the frequency distribution.

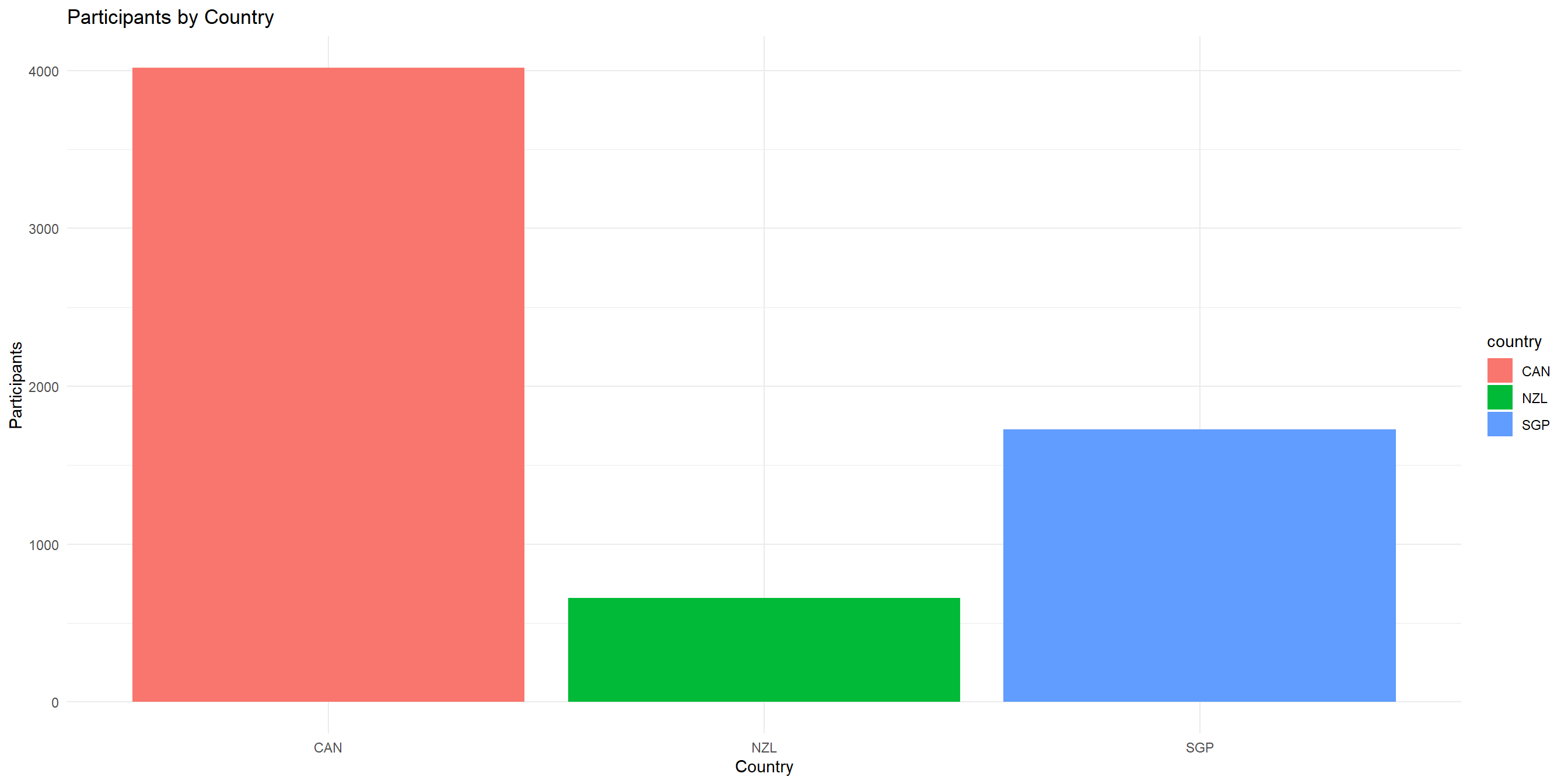
• Let’s visualize the frequency distribution of survey participants by country:

wvs_cleaned |> ggplot(aes(x = country, fill = country)) +
    geom_bar() +
    labs(title = "Participants by Country",
       x = "Country",
       y = "Participants") +
    theme_minimal()

Categorical Data - Bar chart for frequency distribution

Categorical Data - Pie chart for proportion

When we want to show proportion (i.e. in terms of “parts of whole”), we must first quickly calculate the proportion with count()

Let’s create a new dataframe called wvs_country_proportion to hold this data.

wvs_country_proportion <- wvs_cleaned |> 
    group_by(country) |>
    summarize(n = n()) |> # count the number of participants each country
    mutate(proportion = n/sum(n)) # calculate proportion

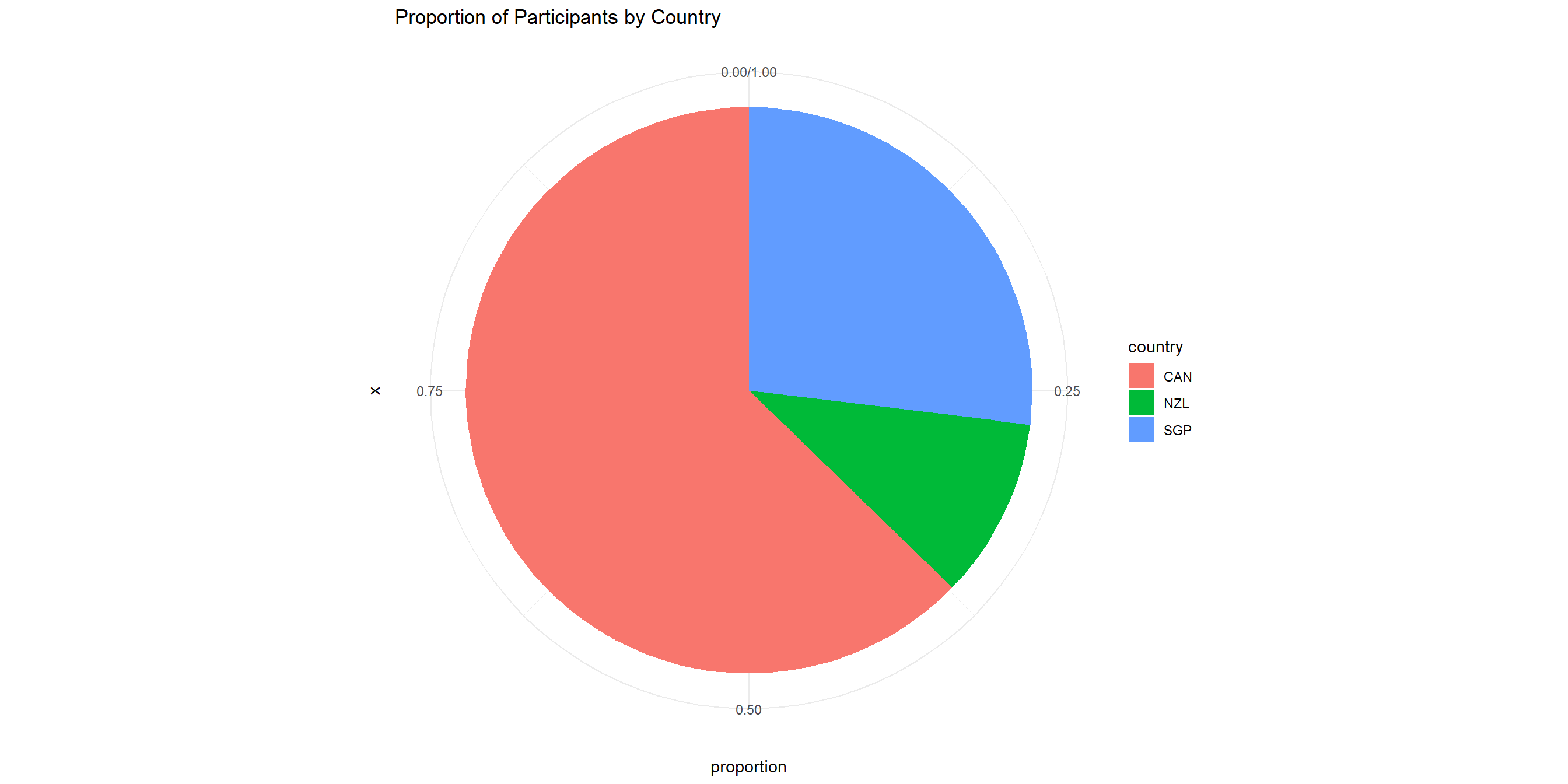
print(wvs_country_proportion)

# A tibble: 3 × 3
  country     n proportion
  <fct>   <int>      <dbl>
1 CAN      4018      0.628
2 NZL       660      0.103
3 SGP      1725      0.269

Categorical Data - Pie chart for proportion

And then, we use this proportion table to create a pie chart by adding coord_polar() layer after geom_bar() and some changes in aes() and geom_bar()

wvs_country_proportion |> ggplot(aes(x = "", y = proportion, fill = country)) +
    geom_bar(stat = "identity", width = 1) +
    coord_polar("y", start = 0) +
    labs(title = "Proportion of Participants by Country") +
    theme_minimal()

Note: if you have lots of categories, pie chart is not always the best option. The code for this pie chart is from R Graph Gallery

Categorical Data - Pie chart for proportion

Learning Check - Grammar of Graphics

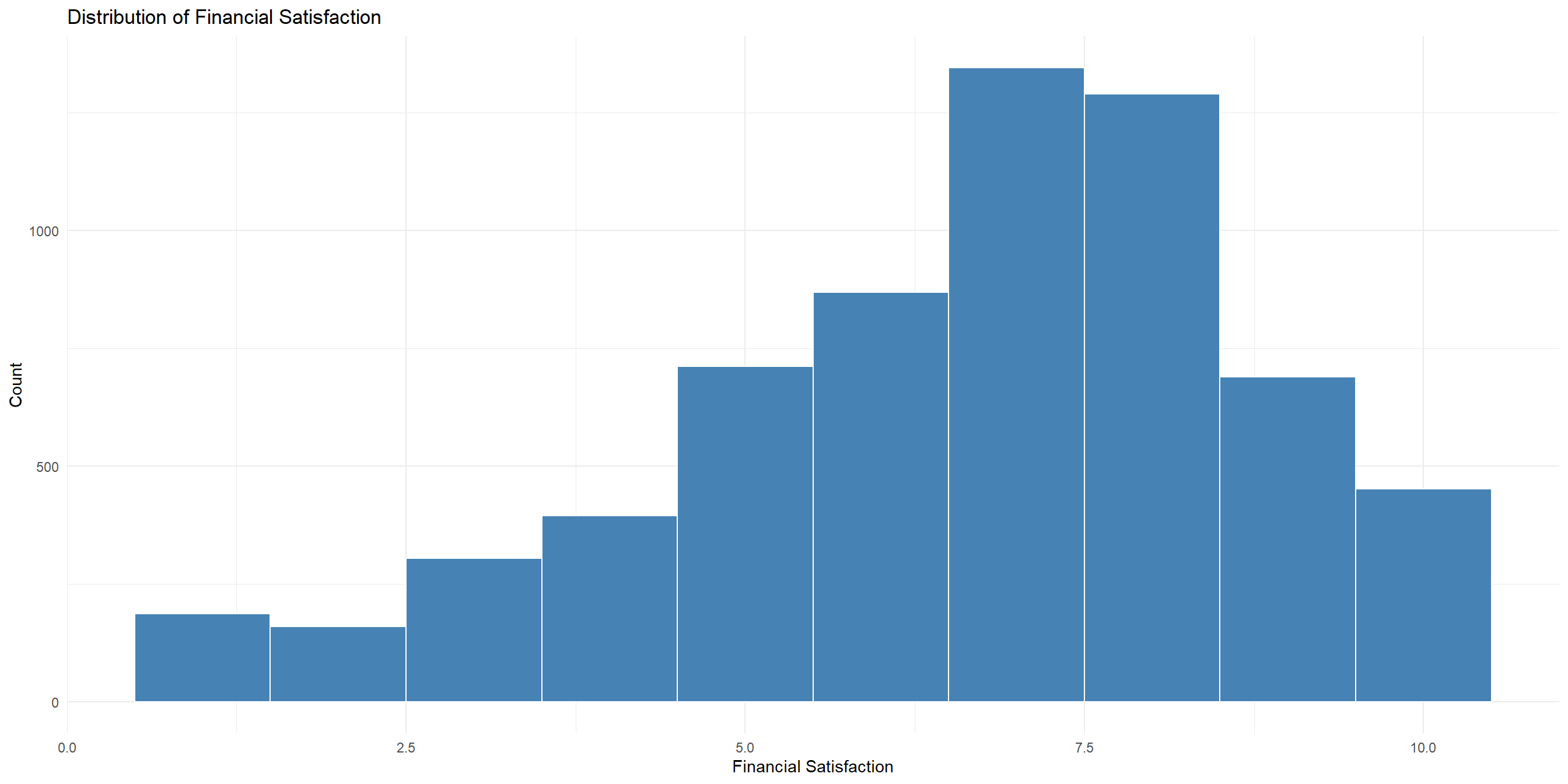
Using the wvs_cleaned dataset:

Create a histogram that visualizes the distribution of financial_satisfaction

wvs_cleaned |> ggplot(aes(x = financial_satisfaction)) +
  geom_histogram(fill = "steelblue", color = "white", binwidth = 1) +
  labs(title = "Distribution of Financial Satisfaction",
       x = "Financial Satisfaction",
       y = "Count") +
  theme_minimal()

Learning Check - Grammar of Graphics

Bivariate Descriptive Stats + Visualization

Three Combinations in Bivariate Descriptive Stats

Bivariate descriptive statistics describe and summarize relationships between two variables in your dataset without making inferences about a larger population. They include numeric measures like correlation or covariance, and visualizations like scatterplots, side-by-side boxplots, or contingency tables.

Think of them as taking a snapshot of how two variables relate to each other in your current data.

Since data can be continuous or categorical, there can be three combinations when we deal with bivariate descriptive stats:

1. Both categorical (e.g. age_group and country)
2. Both continuous (e.g. financial_satisfaction and life_satisfaction)
3. One continuous, one categorical (e.g. country and life_satisfaction)

Both categorical

• Examine relationships between categorical variables

• Look at joint distributions and proportions

• Compare group compositions

First, let’s create a contingency table of age_group and country!

table(wvs_cleaned$age_group, wvs_cleaned$country)

       
         CAN  NZL  SGP
  18-28  712   27  246
  29-44 1232  119  511
  45-60 1061  222  550
  61+   1013  292  418

Both categorical - Proportion table

We can also create a proportion table just like we did earlier

wvs_cleaned |> 
  group_by(country, age_group) |> 
  summarise(n = n()) |> # count the frequency of participants by age group and country 
  mutate(prop = n/sum(n)) # calculate proportion

# A tibble: 12 × 4
# Groups:   country [3]
   country age_group     n   prop
   <fct>   <chr>     <int>  <dbl>
 1 CAN     18-28       712 0.177 
 2 CAN     29-44      1232 0.307 
 3 CAN     45-60      1061 0.264 
 4 CAN     61+        1013 0.252 
 5 NZL     18-28        27 0.0409
 6 NZL     29-44       119 0.180 
 7 NZL     45-60       222 0.336 
 8 NZL     61+         292 0.442 
 9 SGP     18-28       246 0.143 
10 SGP     29-44       511 0.296 
11 SGP     45-60       550 0.319 
12 SGP     61+         418 0.242 

Both categorical - Bar chart

For categorical data like this, we can use barchart to visualize the frequency distribution. Stacked bar chart can be used to visualize proportion.

wvs_cleaned |> ggplot(aes(x = country, fill = age_group)) +
  geom_bar(position = "dodge") + 
  labs(y = "Count", title = "Age Groups by Country") +
  theme_minimal()

Both categorical - Bar chart

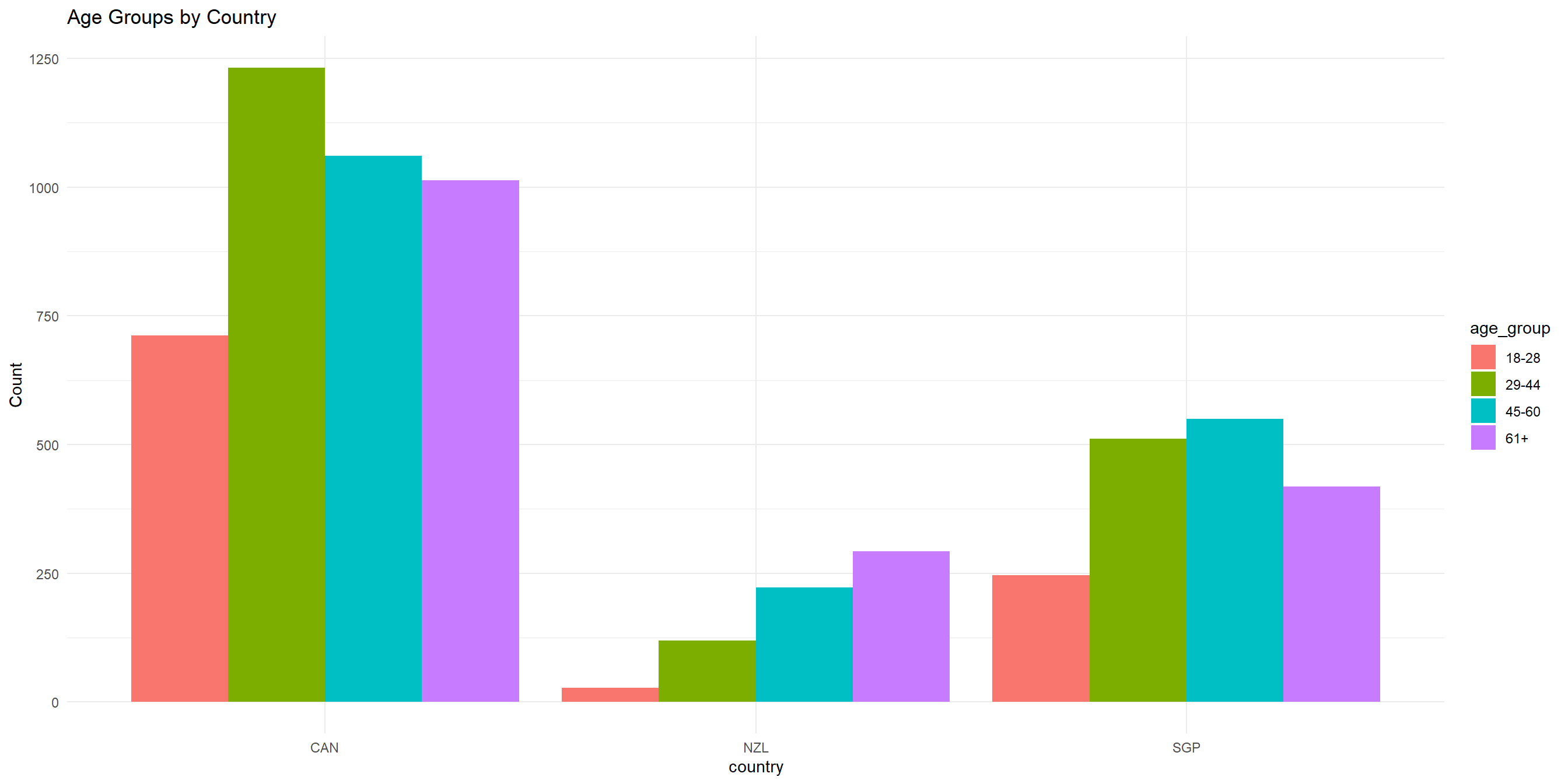
Both categorical - Stacked bar chart

Change position = "dodge" to position = "stack" to stack the bar chart

wvs_cleaned |> ggplot(aes(x = country, fill = age_group)) +
  geom_bar(position = "stack") + 
  labs(y = "Count", title = "Age Groups by Country") +
  theme_minimal()

Both categorical - Stacked bar chart

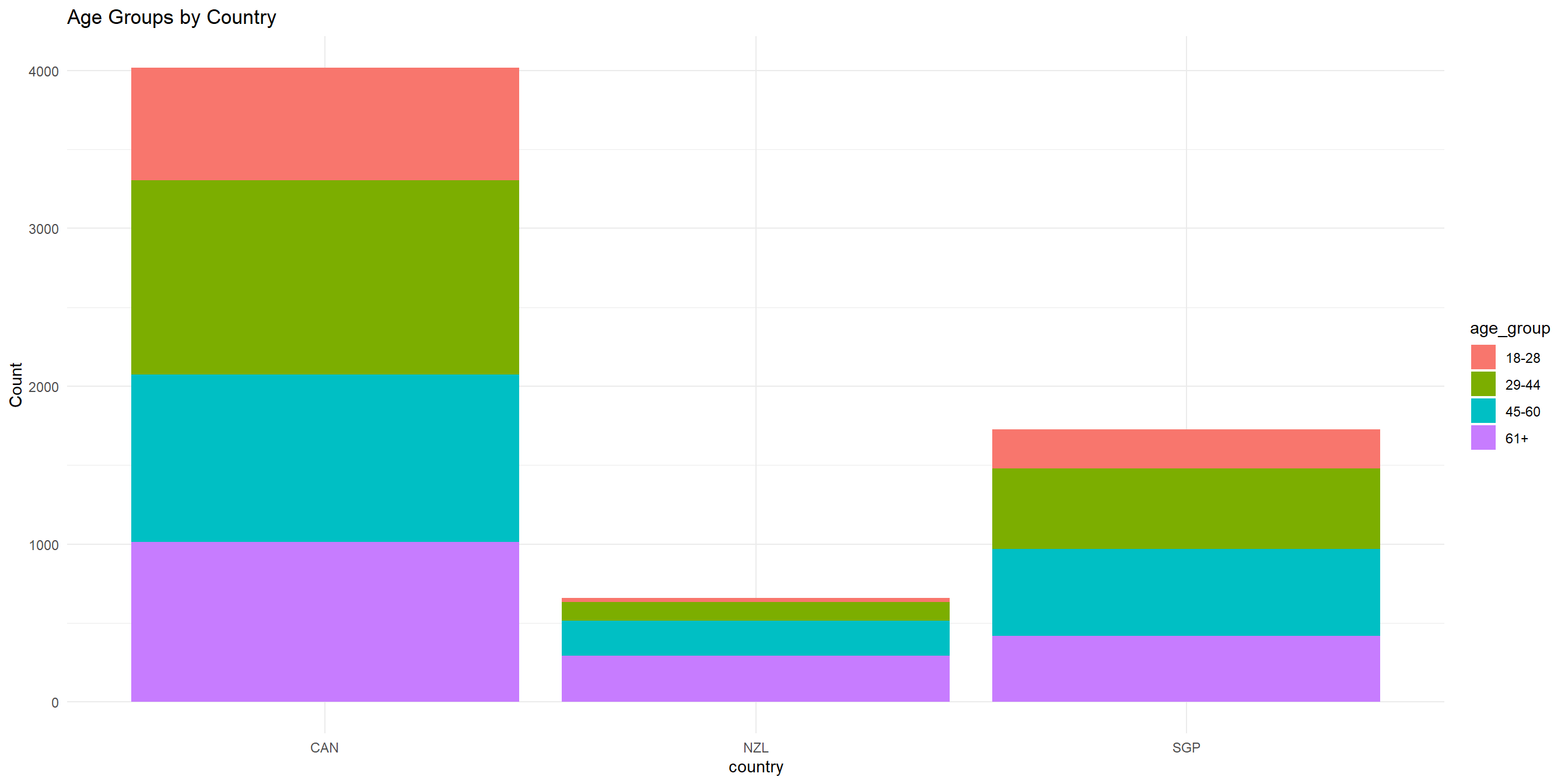
Both categorical - Percent-stacked bar chart

To get a better sense of the proportion for each country, we can use percent stacked bar chart.

The code is similar to previous bar charts; we just have to change the position argument to position = "fill"

wvs_cleaned |> ggplot(aes(x = country, fill = age_group)) +
  geom_bar(position = "fill") + 
  labs(y = "Proportion", title = "Age Groups by Country") +
  theme_minimal()

Both categorical - Percent-stacked bar chart

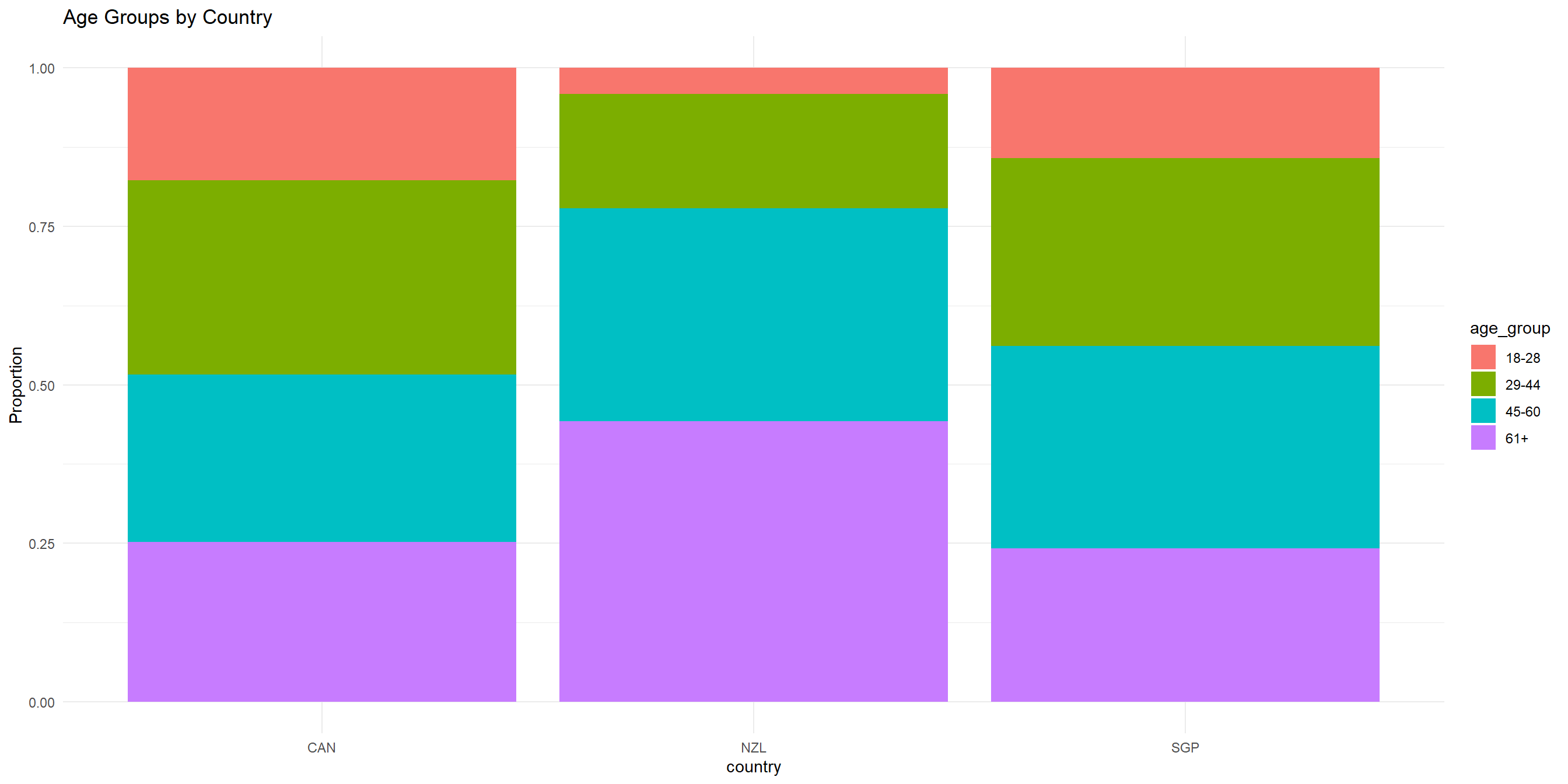
Both continuous

• Examine linear relationships

• Look for patterns and trends

• Identify potential outliers

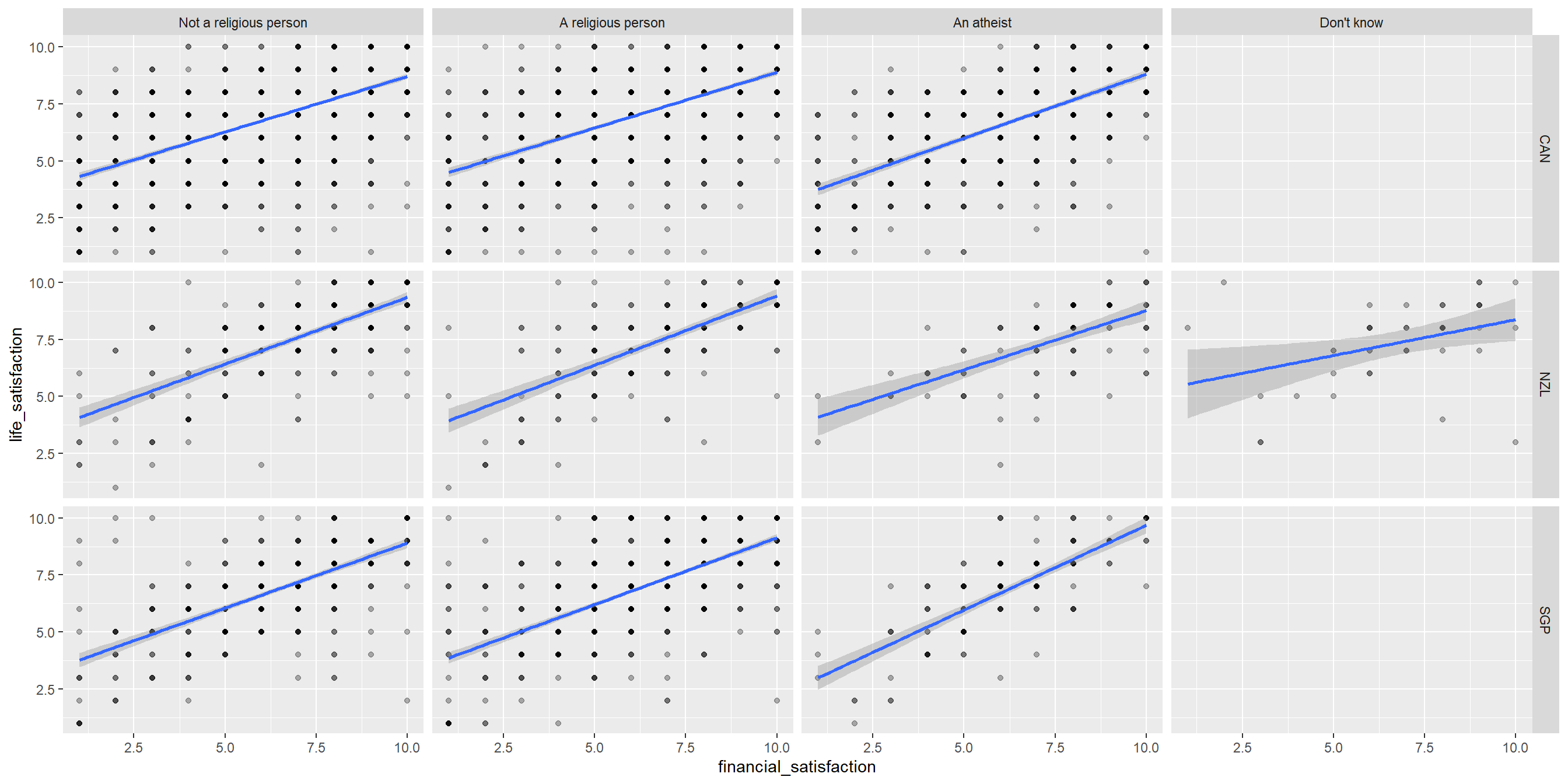
Let’s first examine the correlation between financial_satisfaction and life_satisfaction

cor(wvs_cleaned$financial_satisfaction, wvs_cleaned$life_satisfaction)

[1] 0.6420311

Both continuous - Jitter / scatterplot

Let’s visualize the two variables together with a jitter / scatterplot!

wvs_cleaned |> ggplot(aes(x = financial_satisfaction, y = life_satisfaction)) +
  geom_jitter(alpha = 0.3) +
  geom_smooth(method = "lm") + # layer with geom_smooth
  labs(title = "Financial vs Life Satisfaction") +
  theme_minimal()

Both continuous - Jitter / scatterplot

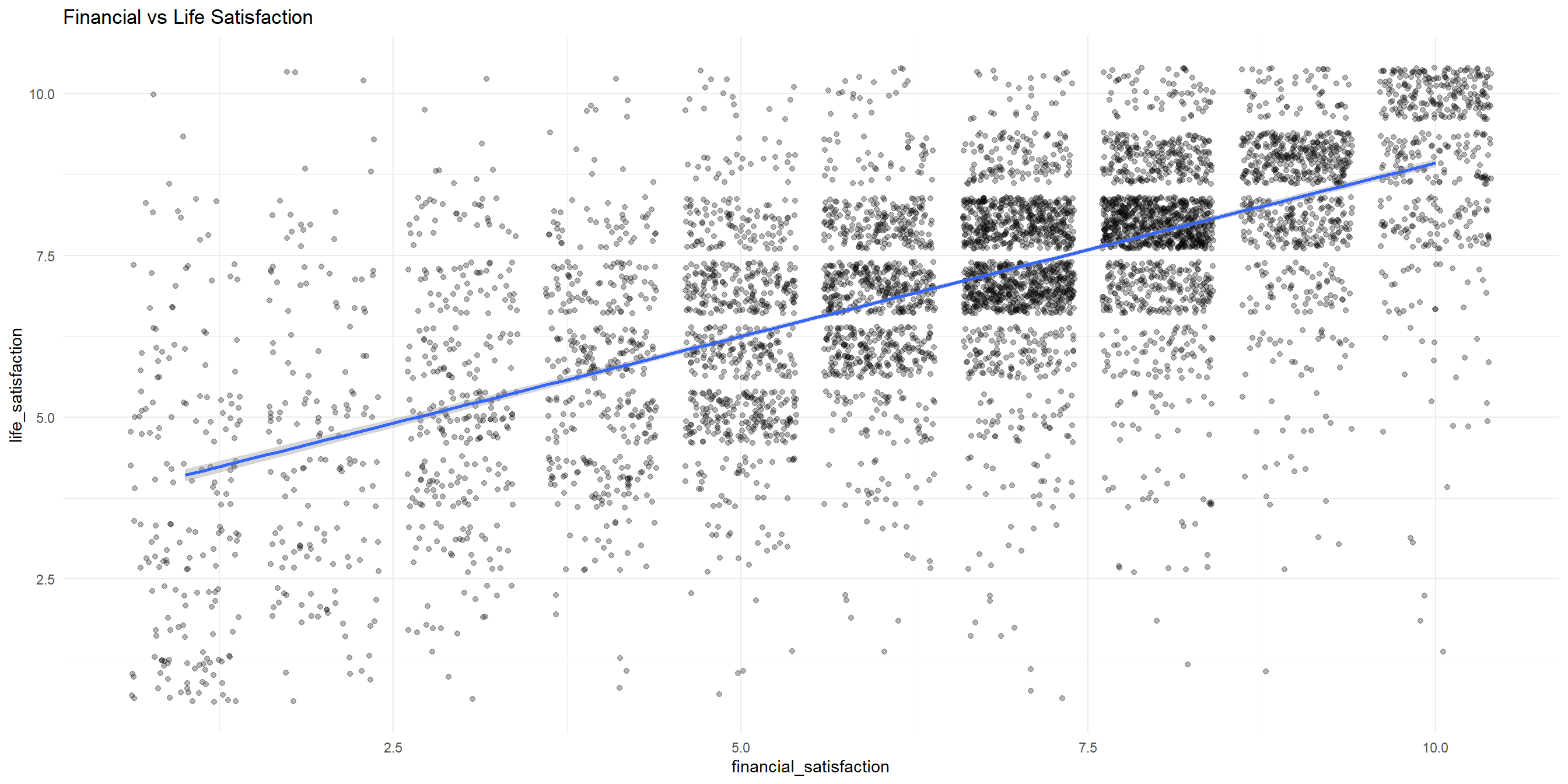
One continuous, one categorical - Summary table

• Compare distributions across groups

• Identify group differences

• Examine spread within groups

Let’s do a recap from last week and get the summary stats for life_satisfaction for each country

wvs_cleaned |> 
  group_by(country) |> 
  summarise(
    mean_satisfaction = mean(life_satisfaction, na.rm = TRUE),
    median_satisfaction = median(life_satisfaction, na.rm = TRUE),
    sd_satisfaction = sd(life_satisfaction, na.rm = TRUE)
  )

# A tibble: 3 × 4
  country mean_satisfaction median_satisfaction sd_satisfaction
  <fct>               <dbl>               <dbl>           <dbl>
1 CAN                  7.04                   7            1.81
2 NZL                  7.60                   8            1.79
3 SGP                  7.06                   7            1.78

One continuous, one categorical - Boxplots

To get a better sense of how the data is varied and spread, let’s visualize them with a side-by-side boxplot

wvs_cleaned |> ggplot(aes(x = country, y = life_satisfaction)) +
  geom_boxplot() +
  labs(title = "Life Satisfaction by Country") +
  theme_minimal()

One continuous, one categorical - Boxplots

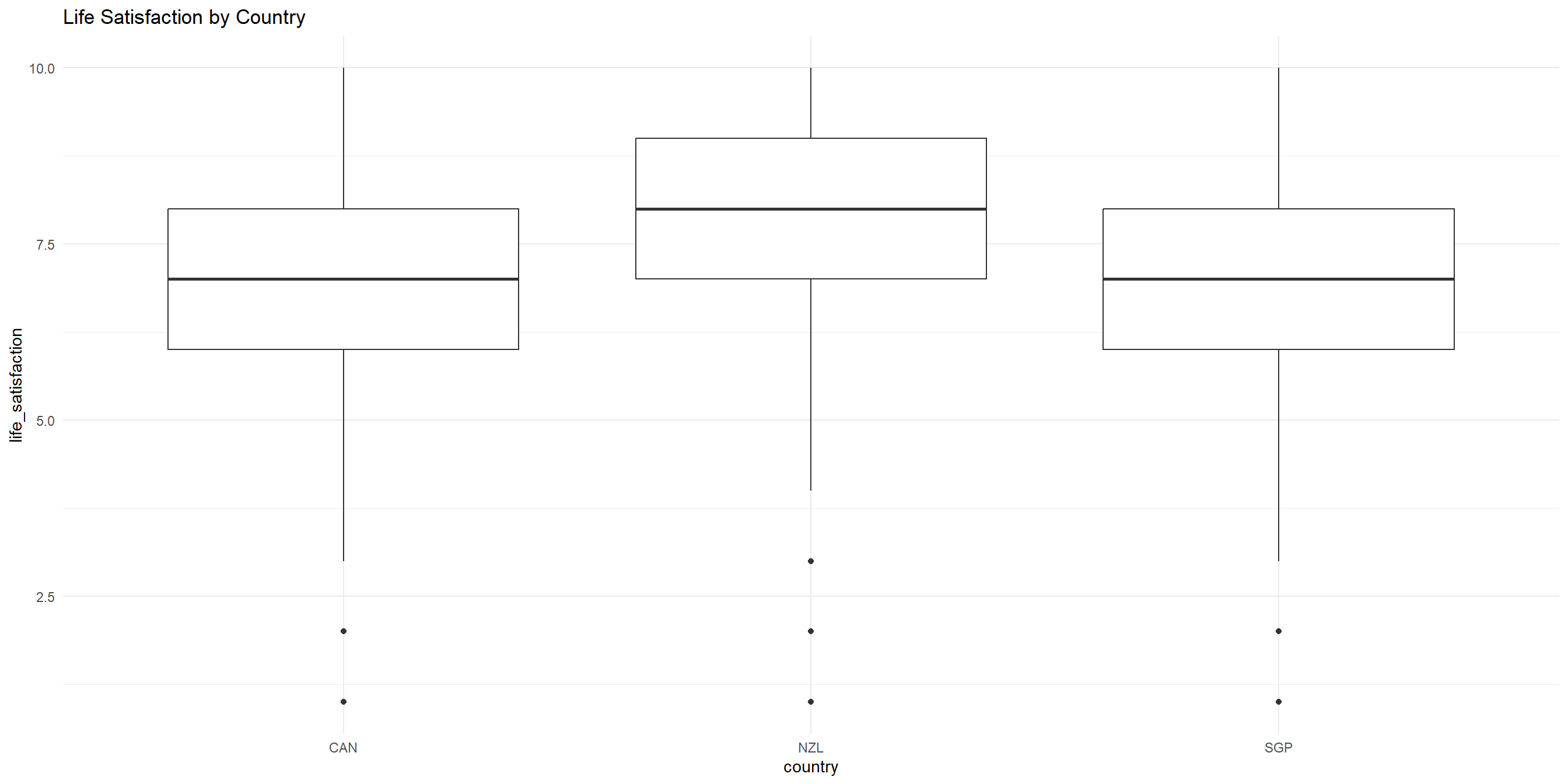
One continuous, one categorical (cont’d) - Layered boxplots and violin plots

We could also layer our boxplots with violin plots to get a better sense of the distribution of each group.

wvs_cleaned |> ggplot(aes(x = country, y = life_satisfaction)) +
  geom_violin(fill = "lightblue", alpha = 0.5) +
  geom_boxplot(width = 0.1, fill = "white") +
  labs(title = "Life Satisfaction Distribution by Country") +
  theme_minimal()

One continuous, one categorical (cont’d) - Layered boxplots and violin plots

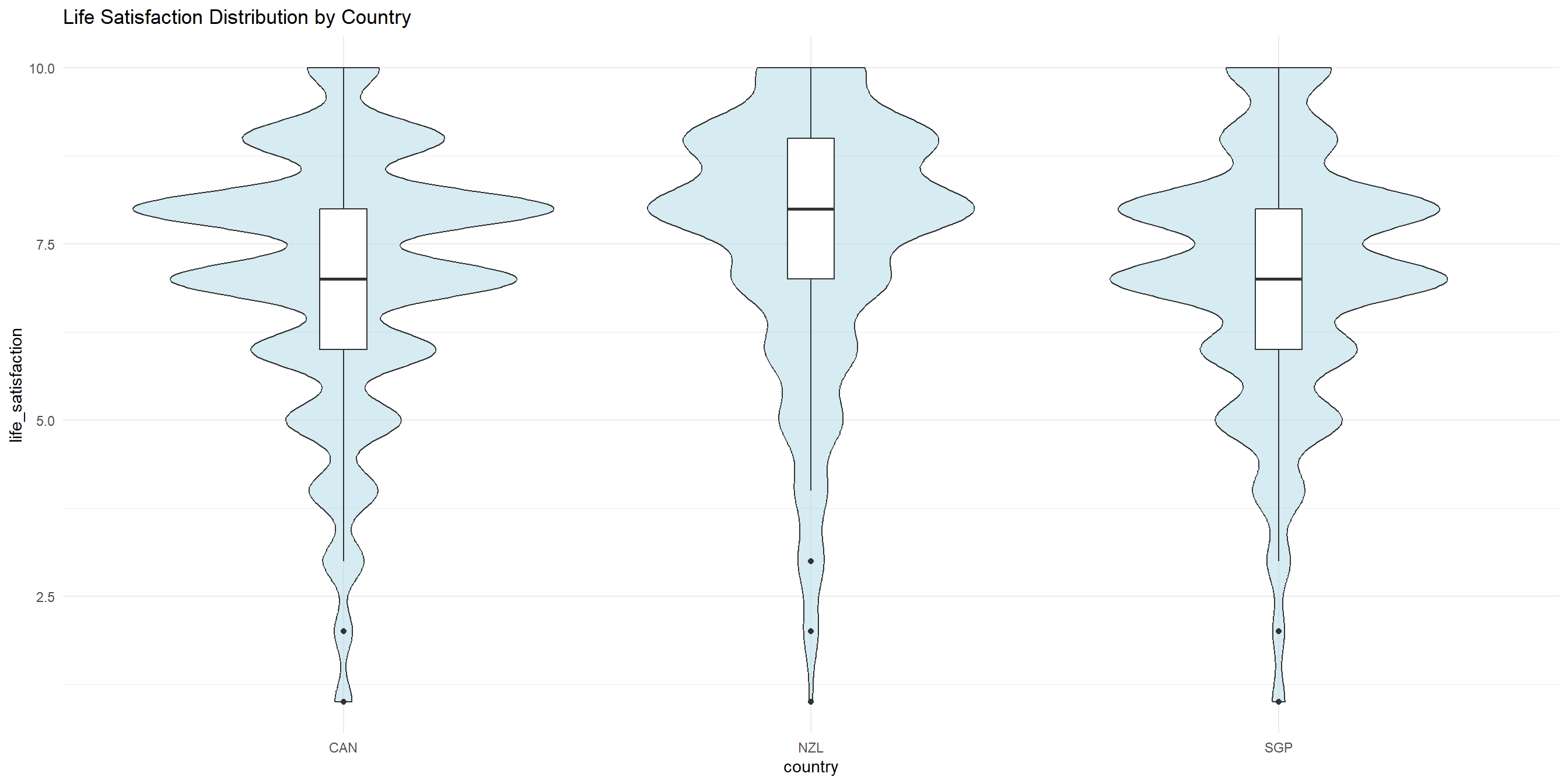
How to save your images - ggsave

There are two ways to do this:

1. Via ggsave

2. The point-and-click way in RStudio

Below is the ggsave way:

# save the chart into an object instead of viewing it like we have been doing
boxplot_obj <- wvs_cleaned |> 
    ggplot(aes(x = age)) +
    geom_boxplot(fill = "lightblue", color = "navy") +
    labs(title = "Age distribution of respondents",
         x = "Age") +
    theme_minimal()

# pass the saved chart into ggsave and give it a filename
ggsave("fig-output/boxplot_1.jpg", boxplot_obj) 

How to save your images - point-and-click

1. Go to plots tab at the right pane
2. Click on Export button. You can export the plot as image file, or as PDF.
3. Important: to keep your files organized, keep your exported images into the fig-output folder that you’ve created in Session 1.

Using Facets for more complex visualization

• Compare patterns across multiple subgroups

• Identify interaction effects

• Maintain visual clarity with complex relationships

Facet grids are useful when we have more than two variables to visualize. However, if used excessively they may become too complex

wvs_cleaned |> ggplot(aes(x = financial_satisfaction, y = life_satisfaction)) +
  geom_point(alpha = 0.3) +
  geom_smooth(method = "lm") +
  facet_grid(country ~ religiousity)

Using Facets for more complex visualization

Is fancier = better?

Fancier, more complicated visualization does not necessarily mean better!

Take a look at this award-winning visualization by Simon Scarr

End of Session 3!

Remember the strategy:

1. Have the ggplot documentation/cheatsheet open
2. Decide on how many variables are involved. Is it just one? two? more than two?
3. Determine whether the variables are categorical or continuous. If you have more than one, are they both categorical? one categorical + one continuous?
4. Refer to the documentation to see which type of visualization would make sense for your variables.

Check out the R Graph gallery for inspiration and code samples!

Next session: inferential stats in R using WVS data

Appendix

At home exercise #1

Create a barchart that visualizes the frequency of religiousity

wvs_cleaned |> ggplot(aes(x = religiousity, fill = religiousity)) +
  geom_bar() +
  labs(title = "Frequency of Religiosity",
       x = "Religiosity",
       y = "Count") +
  theme_minimal()

At home exercise #1

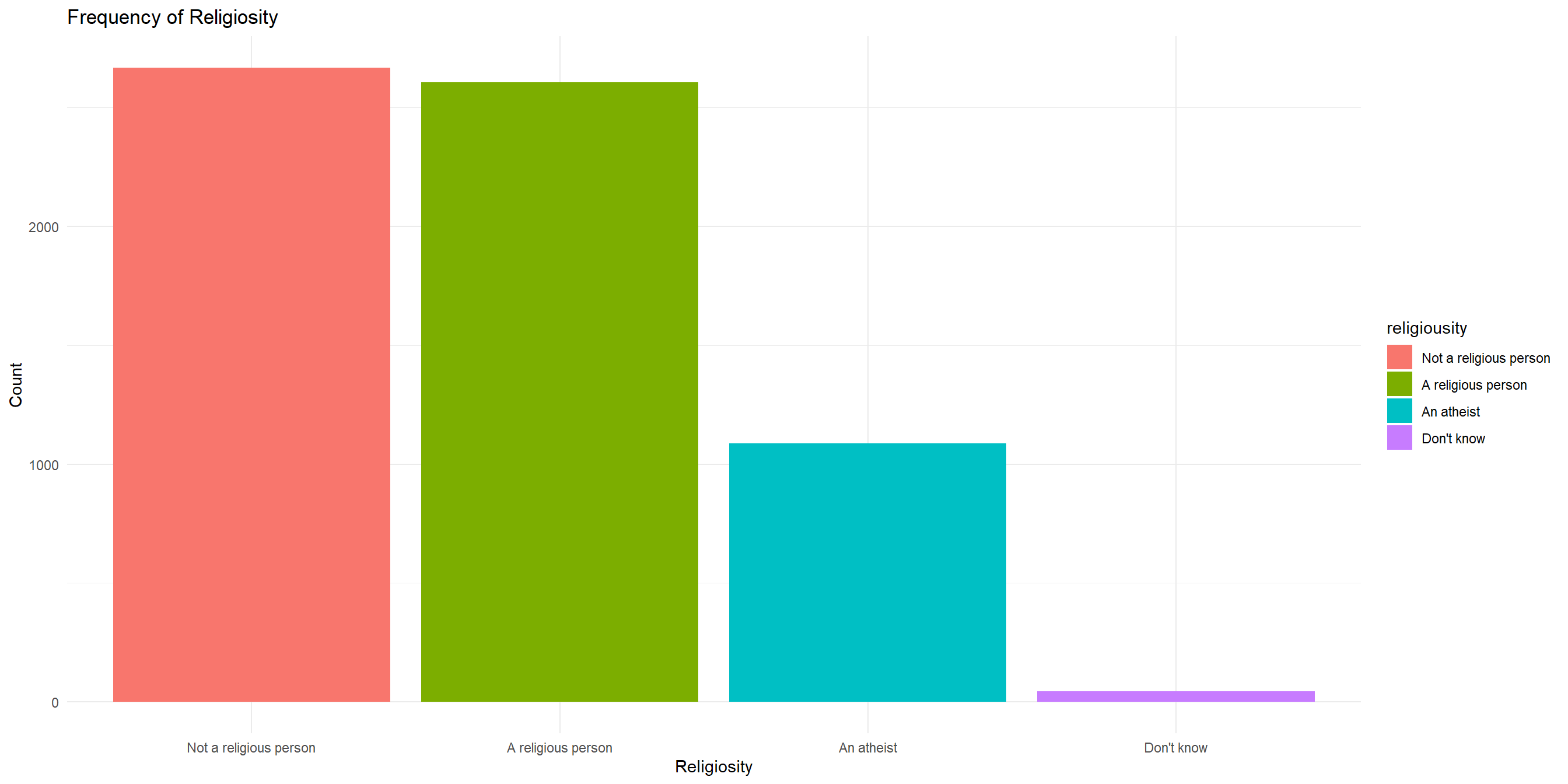
At home exercise #2

Create a side-by-side boxplots that visualizes political_scale for each sex.

wvs_cleaned |> ggplot(aes(x = political_scale, y = sex)) +
  geom_violin(fill = "lightblue", alpha = 0.5) +
  geom_boxplot(width = 0.1, fill = "white") +
  labs(title = "Political scale Distribution by Sex") +
  theme_minimal()

At home exercise #2

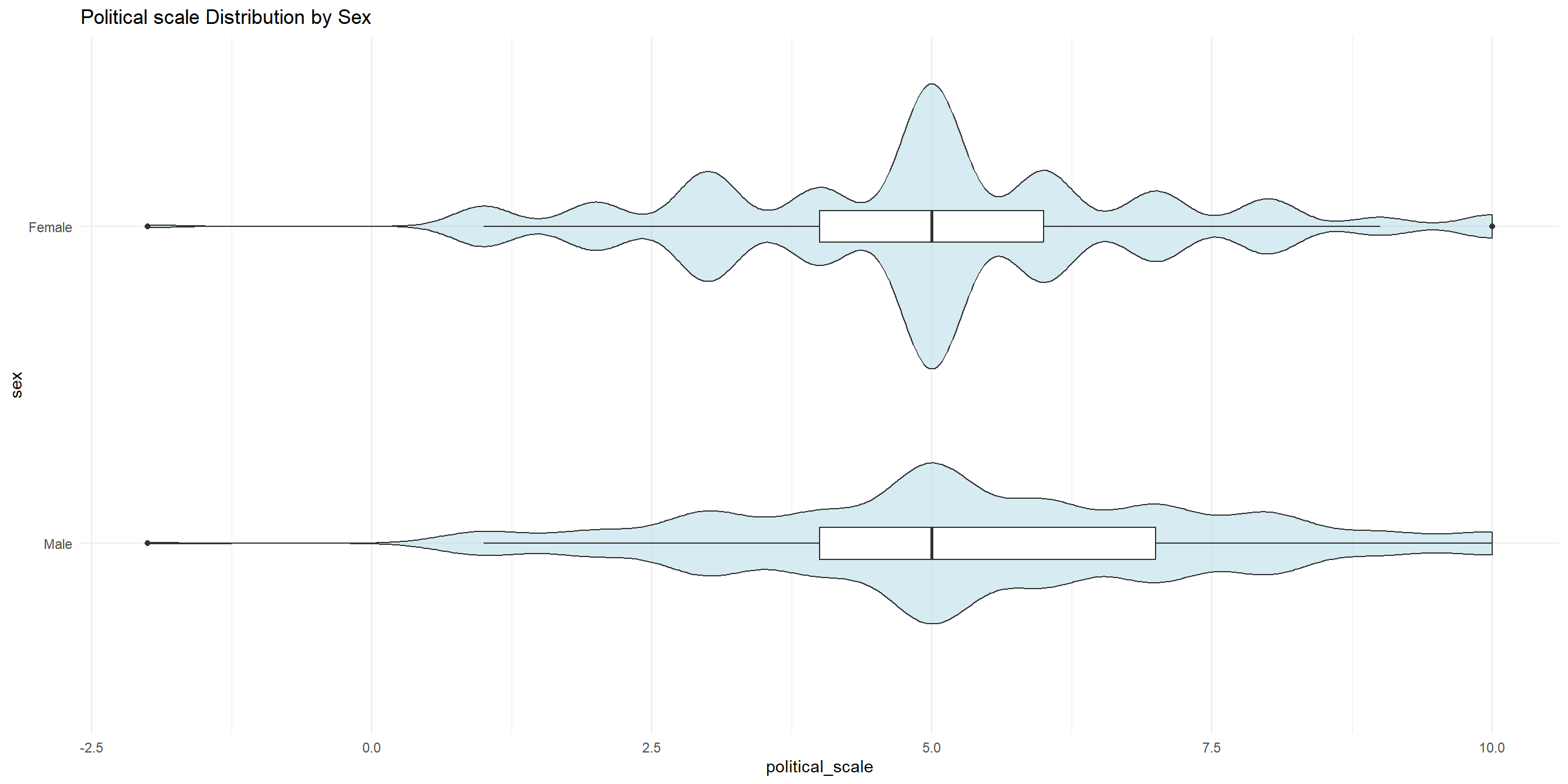
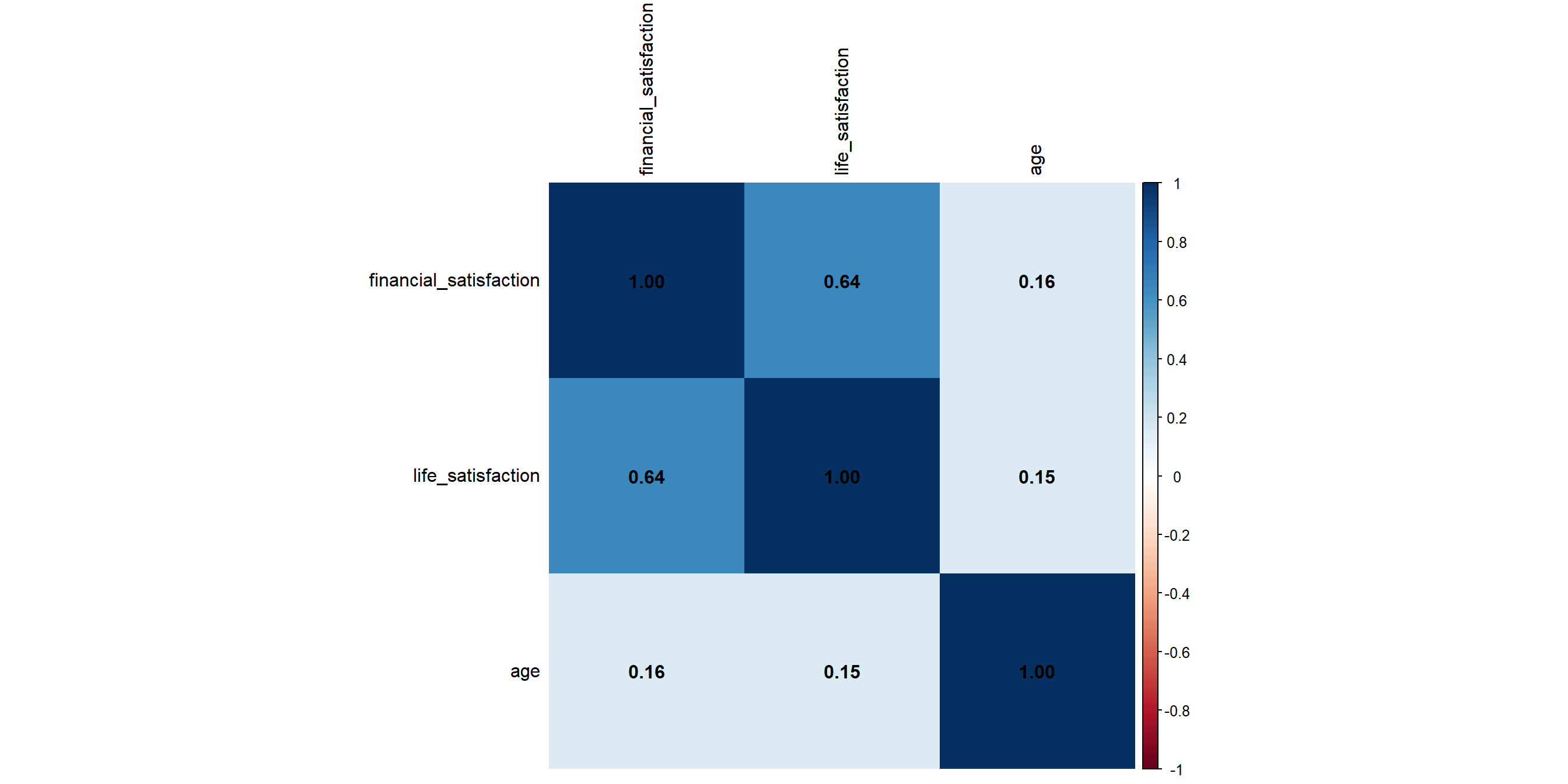
Correlation Plot

When there are more than two continuous variables to explore, correlation map is sometimes used. We can achieve this with ggplot, but it’s much easier to use the corrplot() function from the corrplot package.

Let’s visualize the correlation map for these three variables.

library(corrplot)

# select all the columns for correlation calculation, save it to columns_for_corr
columns_for_corr <- wvs_cleaned |> 
  select(financial_satisfaction, life_satisfaction, age)

# pass the columns_for_corr to cor() function, and save the result to cor_matrix
cor_matrix <- cor(columns_for_corr)

# visualize the cor_matrix with corrplot()!
corrplot(cor_matrix,
         method = "shade", # show the correlation strength as color shades
         addCoef.col = "black", tl.col = "black") # label the coefficients

if you get an error saying “corrplot function not found” or something along that line, that means you need to install the corrplot package first! Run this line in your RStudio Console (bottom left area): install.packages("corrplot")

Correlation Plot

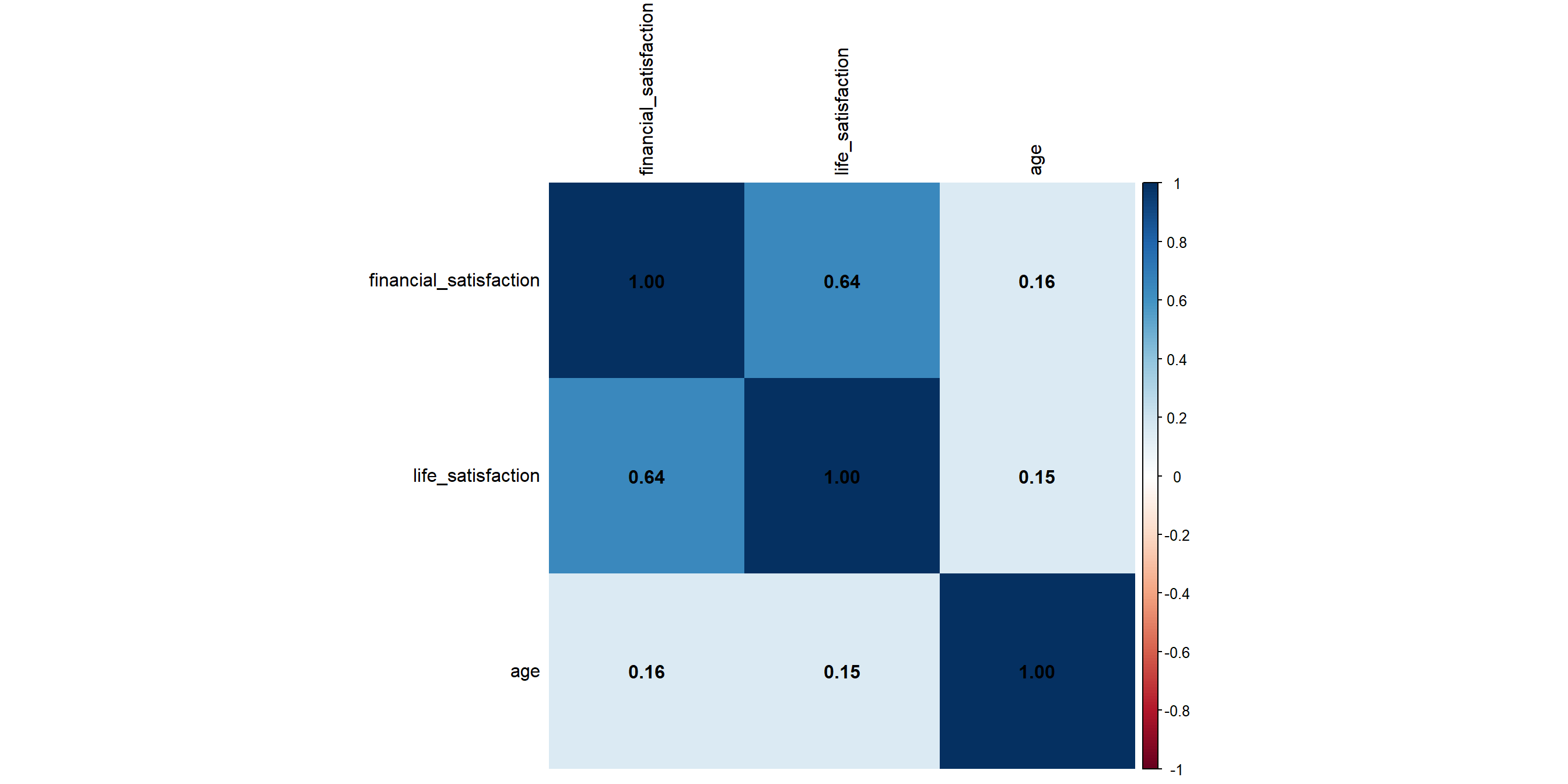
Correlation Plot - shorter code

We can shorten the code in the previous slide using the maggritr pipe |> like so:

wvs_cleaned |> 
    select(financial_satisfaction, life_satisfaction, age) |> 
    cor() |> 
    corrplot(method = "shade", # show the correlation strength as color shades
         addCoef.col = "black", tl.col = "black")

Refresher:

Notice that we don’t have to pass the column names to cor() and corrplot() function. This is because the maggritr pipe |>, acts as a “conveyor belt” that take output from one step and then immediately feed it to the next step.

Correlation Plot - shorter code