Introduction to APIs and statsmodels

+ Putting it all together!

Bella Ratmelia

Recap from last week

Introduction to Pandas dataframe
Datetime in Python and Time Series with Pandas
Visualizing time series with Seaborn

Overview for today

Introduction to FRED API
The statsmodel package for your analysis needs
Your turn: Select an indicator, analyze it, visualize it, and present it to the class!

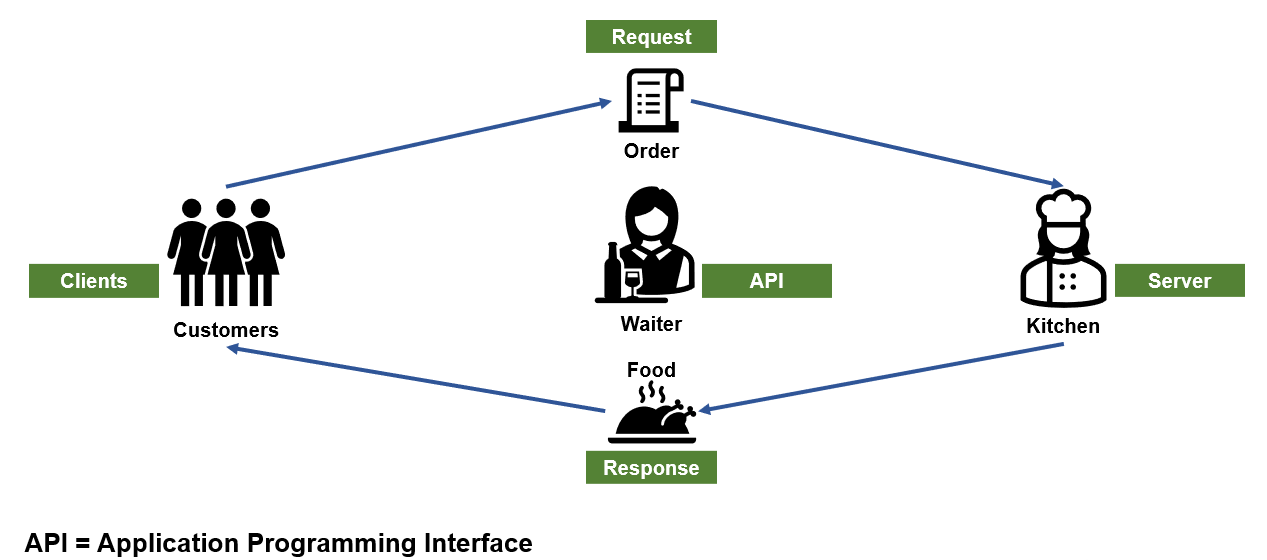
Section 1: Application Programming Interface (API)

What is it?

API (Application Programming Interface) is a set of protocols and tools for building software applications. It defines how different applications interact and communicate.
APIs send requests to servers and receive responses.
Common HTTP methods include GET, POST, PUT, and DELETE. For our use cases, we will primarily use GET.

How to do it in Python

The exact implementations will differ for each API, but this is what it will look like most of the time:

import requests
1api_url = "https://api.example.com/data"
2api_parameters = {
        "query": "hello world",
        "api_key": 12345
    }

3response = requests.get(api_url, params = api_parameters)
4data = response.json()

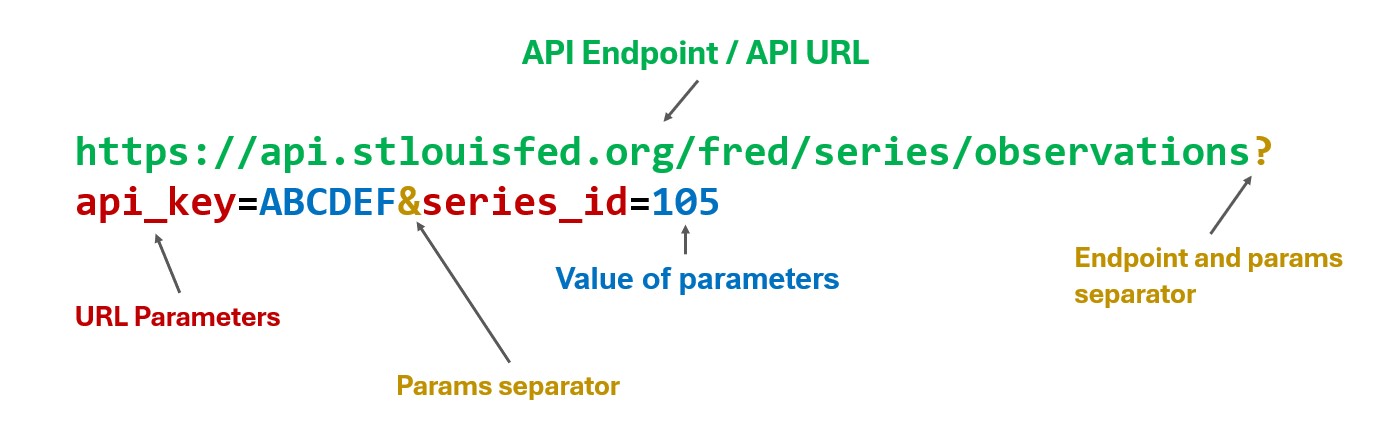
1: The API URL or “endpoint”
2: API Parameters. This varies by API and are typically formatted as a dictionary. When combined with the endpoint URL, the result looks like: https://api.example.com/data?api_key=12345&query=hello%20world
3: Calling the API by passing the api endpoint and the parameters, if any.
4: The api result will be returned in JSON (JavaScript Object Notation) format, which resembles the dictionary data structure in Python.

What does a JSON look like?

Let’s try calling this Public API URL that will give us random fun & useless facts. This API does not require any parameters.

import requests

api_url = "https://uselessfacts.jsph.pl/api/v2/facts/random" 
response = requests.get(api_url) 
if response.status_code == 200: # making sure the call is succesful. Any other status beside 200 means the API call failed.
    data = response.json()

If we print data, this is how it should look like:

{'id': '583be934245210ba8bdb30e604746b09',
 'language': 'en',
 'permalink': 'https://uselessfacts.jsph.pl/api/v2/facts/583be934245210ba8bdb30e604746b09',
 'source': 'djtech.net',
 'source_url': 'http://www.djtech.net/humor/useless_facts.htm',
 'text': 'The word "Checkmate" in chess comes from the Persian phrase "Shah '
         'Mat," which means "the king is dead."'}

Federal Reserve Economic Data (FRED) API

FRED (Federal Reserve Economic Data) is a database maintained by the Federal Reserve Bank of St. Louis, providing access to a wide range of economic data series.

The FRED API allows programmatic access to this data.

Required: Get your API key

To use the FRED API, you need to create an account and obtain an API key from the FRED website. This key authenticates your requests to the API. Click here to create an account and get your key.

Always refer to documentation!

The documentation for FRED API is available here: https://fred.stlouisfed.org/docs/api/fred/

Remember, different API will have their own documentation. Other APIs such as EconDB or SingStat will have their own specifications, so be sure to check the documentation.

Best Practice: How to store your API key

Generally, it is best to save your API key in a separate file or in your environment variables. For now, let’s save it in a plain text file (.txt).

In VS Code, click on File > New Text File
Paste just the API key in the newly opened file. The file should contain just the API key and nothing else.
Save this file as api_key.txt
Check that it is located in the same folder level with the rest of your ipynb files.

Reading the api key from plain text

Let’s read our api_key from the plain text file we just created.

1with open('api_key.txt', 'r') as file:
2    fred_key = file.read().strip()

1: Open the plain text file in ‘read’ mode (hence the ‘r’)
2: Read the entire file (which contains the api key) and save the api key into a variable called fred_key

Interacting with FRED API

let’s retrieve the GDP data from 2010 to 2020 from FRED! Based on the documentation, other than api_key and series_id parameter, these are other params that we can supply to FRED API: observation_start, and observation_end. We want the API to return the result as JSON, so we tell the API about this through the file_type parameter.

fred_url = "https://api.stlouisfed.org/fred/series/observations"

fred_params = {
    "series_id": "UNRATE",
    "api_key": fred_key,
    "file_type": "json",
    "observation_start": "2013-01-01",
    "observation_end": "2023-12-31"
}

response = requests.get(fred_url, params = fred_params)

if response.status_code == 200:
    data = response.json()
    print("succesful!")

succesful!

Anatomy of an API request

Check out the result!

Let’s use pprint (pretty print) package so that the JSON is more readable to human eyes. To install this package, type pip install pprint

import pprint
pprint.pprint(data)

{'count': 132,
 'file_type': 'json',
 'limit': 100000,
 'observation_end': '2023-12-31',
 'observation_start': '2013-01-01',
 'observations': [{'date': '2013-01-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '8.0'},
                  {'date': '2013-02-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '7.7'},
                  {'date': '2013-03-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '7.5'},
                  {'date': '2013-04-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '7.6'},
                  {'date': '2013-05-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '7.5'},
                  {'date': '2013-06-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '7.5'},
                  {'date': '2013-07-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '7.3'},
                  {'date': '2013-08-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '7.2'},
                  {'date': '2013-09-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '7.2'},
                  {'date': '2013-10-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '7.2'},
                  {'date': '2013-11-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '6.9'},
                  {'date': '2013-12-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '6.7'},
                  {'date': '2014-01-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '6.6'},
                  {'date': '2014-02-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '6.7'},
                  {'date': '2014-03-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '6.7'},
                  {'date': '2014-04-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '6.2'},
                  {'date': '2014-05-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '6.3'},
                  {'date': '2014-06-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '6.1'},
                  {'date': '2014-07-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '6.2'},
                  {'date': '2014-08-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '6.1'},
                  {'date': '2014-09-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '5.9'},
                  {'date': '2014-10-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '5.7'},
                  {'date': '2014-11-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '5.8'},
                  {'date': '2014-12-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '5.6'},
                  {'date': '2015-01-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '5.7'},
                  {'date': '2015-02-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '5.5'},
                  {'date': '2015-03-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '5.4'},
                  {'date': '2015-04-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '5.4'},
                  {'date': '2015-05-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '5.6'},
                  {'date': '2015-06-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '5.3'},
                  {'date': '2015-07-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '5.2'},
                  {'date': '2015-08-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '5.1'},
                  {'date': '2015-09-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '5.0'},
                  {'date': '2015-10-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '5.0'},
                  {'date': '2015-11-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '5.1'},
                  {'date': '2015-12-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '5.0'},
                  {'date': '2016-01-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '4.8'},
                  {'date': '2016-02-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '4.9'},
                  {'date': '2016-03-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '5.0'},
                  {'date': '2016-04-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '5.1'},
                  {'date': '2016-05-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '4.8'},
                  {'date': '2016-06-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '4.9'},
                  {'date': '2016-07-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '4.8'},
                  {'date': '2016-08-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '4.9'},
                  {'date': '2016-09-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '5.0'},
                  {'date': '2016-10-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '4.9'},
                  {'date': '2016-11-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '4.7'},
                  {'date': '2016-12-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '4.7'},
                  {'date': '2017-01-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '4.7'},
                  {'date': '2017-02-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '4.6'},
                  {'date': '2017-03-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '4.4'},
                  {'date': '2017-04-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '4.4'},
                  {'date': '2017-05-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '4.4'},
                  {'date': '2017-06-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '4.3'},
                  {'date': '2017-07-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '4.3'},
                  {'date': '2017-08-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '4.4'},
                  {'date': '2017-09-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '4.3'},
                  {'date': '2017-10-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '4.2'},
                  {'date': '2017-11-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '4.2'},
                  {'date': '2017-12-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '4.1'},
                  {'date': '2018-01-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '4.0'},
                  {'date': '2018-02-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '4.1'},
                  {'date': '2018-03-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '4.0'},
                  {'date': '2018-04-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '4.0'},
                  {'date': '2018-05-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '3.8'},
                  {'date': '2018-06-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '4.0'},
                  {'date': '2018-07-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '3.8'},
                  {'date': '2018-08-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '3.8'},
                  {'date': '2018-09-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '3.7'},
                  {'date': '2018-10-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '3.8'},
                  {'date': '2018-11-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '3.8'},
                  {'date': '2018-12-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '3.9'},
                  {'date': '2019-01-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '4.0'},
                  {'date': '2019-02-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '3.8'},
                  {'date': '2019-03-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '3.8'},
                  {'date': '2019-04-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '3.7'},
                  {'date': '2019-05-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '3.6'},
                  {'date': '2019-06-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '3.6'},
                  {'date': '2019-07-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '3.7'},
                  {'date': '2019-08-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '3.6'},
                  {'date': '2019-09-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '3.5'},
                  {'date': '2019-10-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '3.6'},
                  {'date': '2019-11-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '3.6'},
                  {'date': '2019-12-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '3.6'},
                  {'date': '2020-01-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '3.6'},
                  {'date': '2020-02-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '3.5'},
                  {'date': '2020-03-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '4.4'},
                  {'date': '2020-04-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '14.8'},
                  {'date': '2020-05-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '13.2'},
                  {'date': '2020-06-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '11.0'},
                  {'date': '2020-07-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '10.2'},
                  {'date': '2020-08-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '8.4'},
                  {'date': '2020-09-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '7.8'},
                  {'date': '2020-10-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '6.8'},
                  {'date': '2020-11-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '6.7'},
                  {'date': '2020-12-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '6.7'},
                  {'date': '2021-01-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '6.4'},
                  {'date': '2021-02-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '6.2'},
                  {'date': '2021-03-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '6.1'},
                  {'date': '2021-04-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '6.1'},
                  {'date': '2021-05-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '5.8'},
                  {'date': '2021-06-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '5.9'},
                  {'date': '2021-07-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '5.4'},
                  {'date': '2021-08-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '5.1'},
                  {'date': '2021-09-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '4.7'},
                  {'date': '2021-10-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '4.5'},
                  {'date': '2021-11-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '4.1'},
                  {'date': '2021-12-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '3.9'},
                  {'date': '2022-01-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '4.0'},
                  {'date': '2022-02-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '3.8'},
                  {'date': '2022-03-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '3.6'},
                  {'date': '2022-04-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '3.7'},
                  {'date': '2022-05-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '3.6'},
                  {'date': '2022-06-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '3.6'},
                  {'date': '2022-07-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '3.5'},
                  {'date': '2022-08-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '3.6'},
                  {'date': '2022-09-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '3.5'},
                  {'date': '2022-10-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '3.6'},
                  {'date': '2022-11-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '3.6'},
                  {'date': '2022-12-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '3.5'},
                  {'date': '2023-01-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '3.4'},
                  {'date': '2023-02-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '3.6'},
                  {'date': '2023-03-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '3.5'},
                  {'date': '2023-04-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '3.4'},
                  {'date': '2023-05-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '3.7'},
                  {'date': '2023-06-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '3.6'},
                  {'date': '2023-07-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '3.5'},
                  {'date': '2023-08-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '3.8'},
                  {'date': '2023-09-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '3.8'},
                  {'date': '2023-10-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '3.8'},
                  {'date': '2023-11-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '3.7'},
                  {'date': '2023-12-01',
                   'realtime_end': '2024-10-10',
                   'realtime_start': '2024-10-10',
                   'value': '3.7'}],
 'offset': 0,
 'order_by': 'observation_date',
 'output_type': 1,
 'realtime_end': '2024-10-10',
 'realtime_start': '2024-10-10',
 'sort_order': 'asc',
 'units': 'lin'}

The API returns a lot of information, but what we want to save is the observations, specifically the date and value columns.

Sieve results and save to CSV

What we want to save is the observations, specifically the date and value columns.

import pandas as pd

1unemployment_df = pd.DataFrame(data['observations'])
2unemployment_df = unemployment_df.drop(['realtime_start', 'realtime_end'], axis=1)
3unemployment_df.to_csv("data/unemployment-via-api.csv")

1: Get the values stored under observations label and save it into unemployment_df dataframe.
2: As there are extra columns that we don’t need, drop them.
3: Save the api result into a CSV for reuse later.

The easier way: FRED API wrapper, `fredapi` package

The fredapi package is a Python wrapper for the FRED API, making it easier to interact with FRED data in Python. i.e., it can do what we just did in a fewer lines of code.

To install this package, type in pip install fredapi

from fredapi import Fred
import pandas as pd

fred = Fred(api_key=fred_key)

data = fred.get_series('UNRATE', observation_start="2013-01-01", observation_end="2023-12-31")
df_wrapper = pd.DataFrame(data, columns=['value'])
df_wrapper.tail()

The easier way: FRED API wrapper, `fredapi` package

	value
2023-08-01	3.8
2023-09-01	3.8
2023-10-01	3.8
2023-11-01	3.7
2023-12-01	3.7

Merging two (or more) dataframes

When working with multiple data series from FRED, you may want to merge them into a single dataframe for analysis or to save it for later. This is especially important if the API usage costs money (Fortunately FRED is free)

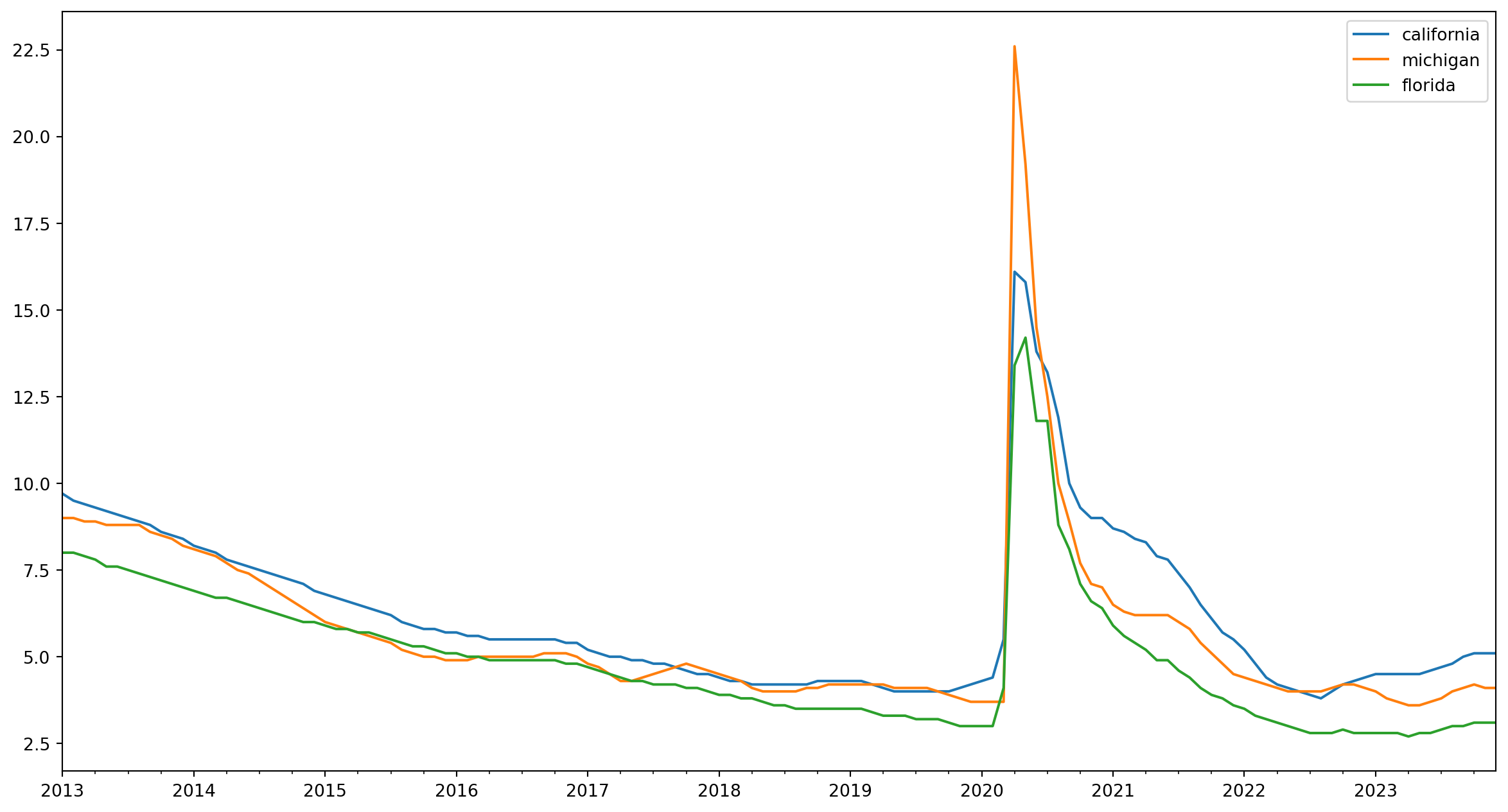
Example: retrieve unemployment rate for California, Michigan, and Florida.

start = "2013-01-01"
end = "2023-12-31"

ca_data = fred.get_series('CAUR', observation_start = start, observation_end = end)
mi_data = fred.get_series('MIUR', observation_start = start, observation_end = end)
fl_data = fred.get_series('FLUR', observation_start = start, observation_end = end)

ca_unrate = pd.DataFrame(ca_data, columns=['california'])
mi_unrate = pd.DataFrame(mi_data, columns=['michigan'])
fl_unrate = pd.DataFrame(fl_data, columns=['florida'])

usa_unrate = pd.merge(ca_unrate, mi_unrate, left_index=True, right_index=True, how='inner')
usa_unrate = pd.merge(usa_unrate, fl_unrate, left_index=True, right_index=True, how='inner')

usa_unrate.tail(10)

Merging two (or more) dataframes

	california	michigan	florida
2023-03-01	4.5	3.7	2.8
2023-04-01	4.5	3.6	2.7
2023-05-01	4.5	3.6	2.8
2023-06-01	4.6	3.7	2.8
2023-07-01	4.7	3.8	2.9
2023-08-01	4.8	4.0	3.0
2023-09-01	5.0	4.1	3.0
2023-10-01	5.1	4.2	3.1
2023-11-01	5.1	4.1	3.1
2023-12-01	5.1	4.1	3.1

Plot them!

usa_unrate.plot()

More APIs to try

Go to Public API GitHub page to see various free public apis to explore!

Economics and Finance-related APIs such as Alpaca, FRED, Yahoo Finance
Government Open Data like Census.gov

Learning Check

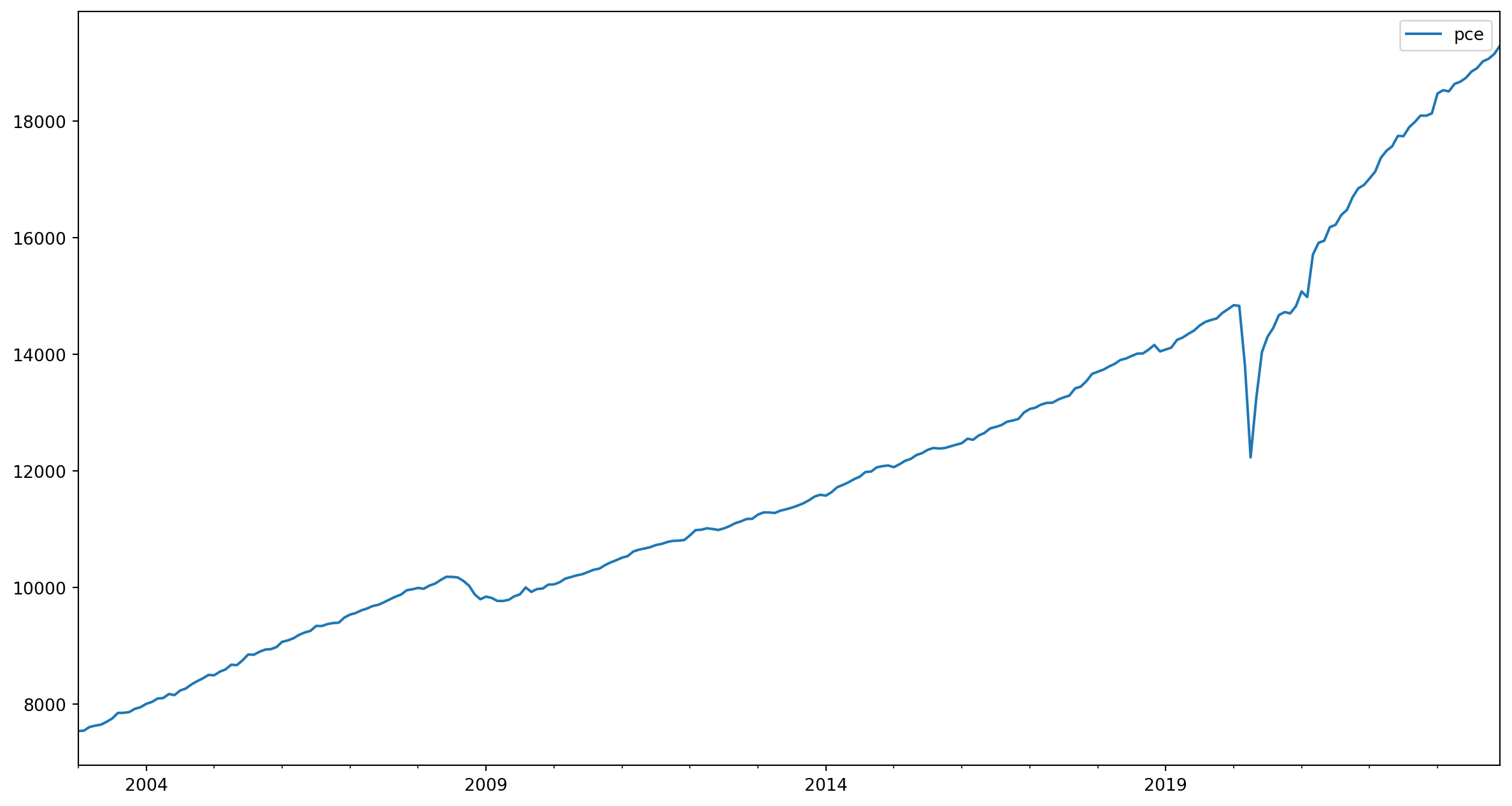
Explore the FRED database and retrieve the Personal Consumption Expenditure for the last 2 decades (2003 to 2023)
Plot the series.

Code

pce_data = fred.get_series('PCE', observation_start = "2003-01-01", observation_end = "2023-12-31")
pce = pd.DataFrame(pce_data, columns = ["pce"])
pce.plot()

Section 2: The statsmodel package

Introduction and where to find the guides

statsmodels is a Python package that provides classes and functions for the estimation of various statistical models, as well as for conducting statistical tests and statistical data exploration.

To install, type pip install statsmodels and execute it.

The documentation gives us a few pointers on how to import this package depending on what we want to use:

import statsmodels.api as sm            # for linear regressions, logit, probit models, etc
import statsmodels.tsa.api as tsa       # Time series models
import statsmodels.formula.api as smf   # Use this if you want to specify the formula directly

# import matplotlib for plotting purposes
import matplotlib.pyplot as plt

Let’s try a simple regression - OLS

Note

Our data is not exactly the right kind for regression. We are doing this for statsmodel demonstration purposes only.

import statsmodels.api as sm
import numpy as np

exog_x = usa_unrate['california']
endo_y = usa_unrate['florida']

usa_model = sm.OLS(endo_y, exog_x).fit()
print(usa_model.summary())

Let’s try a simple regression - OLS

                                 OLS Regression Results                                
=======================================================================================
Dep. Variable:                florida   R-squared (uncentered):                   0.987
Model:                            OLS   Adj. R-squared (uncentered):              0.987
Method:                 Least Squares   F-statistic:                          1.005e+04
Date:                Thu, 10 Oct 2024   Prob (F-statistic):                   1.05e-125
Time:                        16:37:10   Log-Likelihood:                         -121.76
No. Observations:                 132   AIC:                                      245.5
Df Residuals:                     131   BIC:                                      248.4
Df Model:                           1                                                  
Covariance Type:            nonrobust                                                  
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
california     0.8053      0.008    100.238      0.000       0.789       0.821
==============================================================================
Omnibus:                       10.327   Durbin-Watson:                   0.167
Prob(Omnibus):                  0.006   Jarque-Bera (JB):               11.018
Skew:                          -0.680   Prob(JB):                      0.00405
Kurtosis:                       2.609   Cond. No.                         1.00
==============================================================================

Notes:
[1] R² is computed without centering (uncentered) since the model does not contain a constant.
[2] Standard Errors assume that the covariance matrix of the errors is correctly specified.

OLS from `formula` sub-package

We can also call upon the formula sub-pacakge if we want to specify the exact formula for our OLS like so:

import statsmodels.formula.api as smf

usa_model_form = smf.ols("florida ~ california", data = usa_unrate).fit()
print(usa_model_form.summary())

OLS from `formula` sub-package

                            OLS Regression Results                            
==============================================================================
Dep. Variable:                florida   R-squared:                       0.917
Model:                            OLS   Adj. R-squared:                  0.917
Method:                 Least Squares   F-statistic:                     1440.
Date:                Thu, 10 Oct 2024   Prob (F-statistic):           3.48e-72
Time:                        16:37:10   Log-Likelihood:                -119.67
No. Observations:                 132   AIC:                             243.3
Df Residuals:                     130   BIC:                             249.1
Df Model:                           1                                         
Covariance Type:            nonrobust                                         
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
Intercept     -0.3024      0.148     -2.044      0.043      -0.595      -0.010
california     0.8480      0.022     37.942      0.000       0.804       0.892
==============================================================================
Omnibus:                       15.139   Durbin-Watson:                   0.159
Prob(Omnibus):                  0.001   Jarque-Bera (JB):               17.879
Skew:                          -0.894   Prob(JB):                     0.000131
Kurtosis:                       2.767   Cond. No.                         19.0
==============================================================================

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

Let’s try some Time Series analysis

statsmodels comes with a wide range of functions that we can use to conduct common time series analysis such as:

Stationarity test (ADF)
Seasonal Decomposition
Correlation Matrix
ARIMA Modelling (single variable)

All of the time series analysis functions are inside the tsa sub-package of statsmodels. Let’s try these!

Stationarity test (ADF)

mi_stt = tsa.adfuller(usa_unrate['michigan'])
print("results:", mi_stt)
print("ADF statistic:", mi_stt[0])
print("p-value:", mi_stt[1])
print("critical values:")
for key, value in mi_stt[4].items():
    print(key, value)

results: (-4.040152272716747, 0.0012142572247144069, 0, 131, {'1%': -3.481281802271349, '5%': -2.883867891664528, '10%': -2.5786771965503177}, 468.54200914983454)
ADF statistic: -4.040152272716747
p-value: 0.0012142572247144069
critical values:
1% -3.481281802271349
5% -2.883867891664528
10% -2.5786771965503177

The result indicates that the ADF statistics is lower than all critical values and p-value < 0.05, which means we reject null hypothesis (\(H_0\): The time series is non-stationary). The time series for Michigan appears to be stationary.

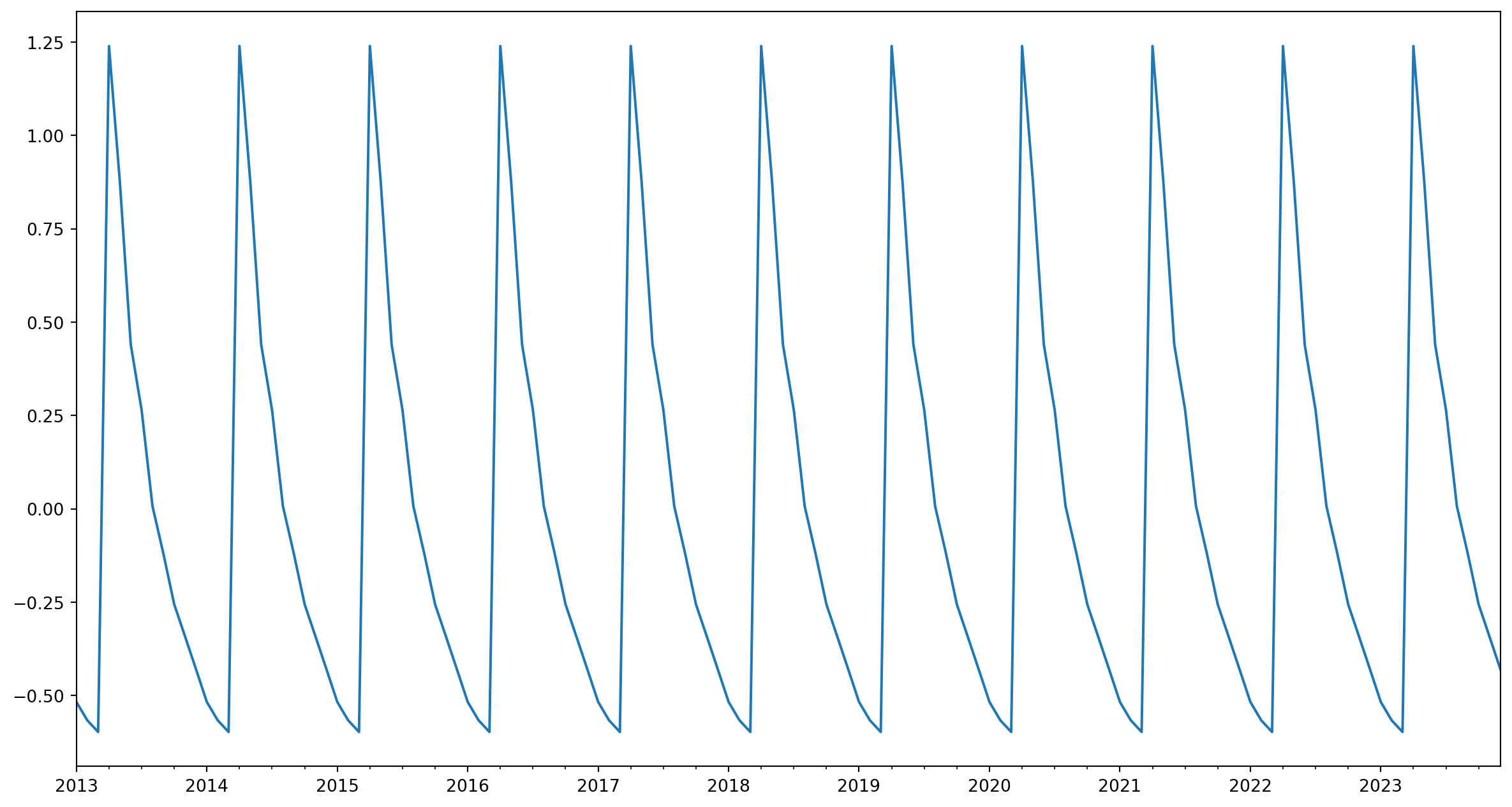
Seasonal Decomposition

The seasonal_decomposition function in statsmodels allows us to decompose a time series into its underlying components: trend (long term movement), seasonal, and residual (or irregular).

Let’s decompose the time series data for Michigan! (It is stationary so this step is not strictly necessary, but let’s do it anyway!)

import statsmodels.tsa.api as tsa

mi_result = tsa.seasonal_decompose(usa_unrate['michigan'], model='additive')
mi_result.plot()
plt.show()

Seasonal Decomposition

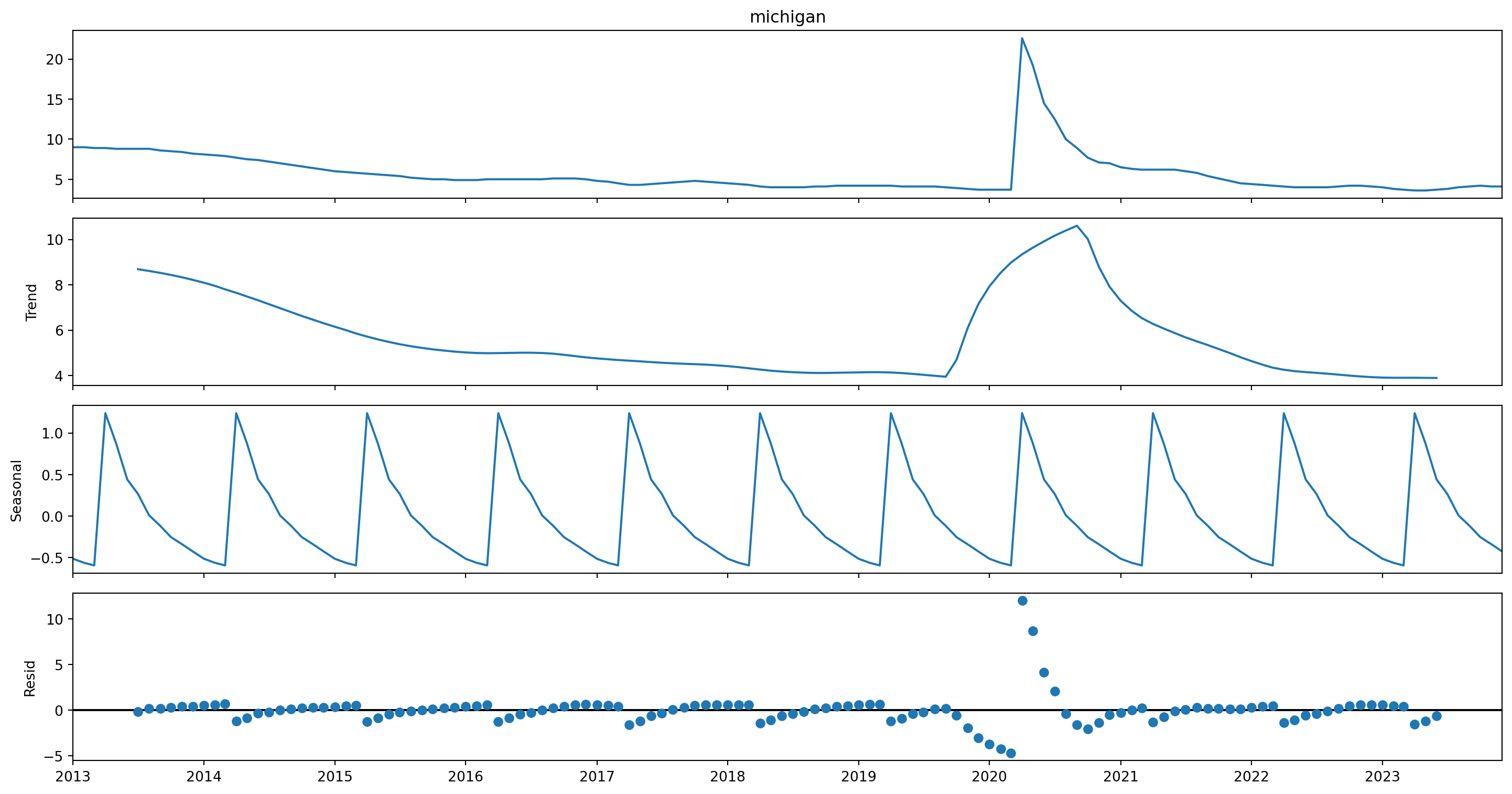
Individually retrieve trends, season, and residuals

To retrieve them individually:

Trend: mi_result.trend.plot()
Seasonality: mi_result.seasonal.plot()
Residuals: mi_result.resid.plot()

mi_result.seasonal.plot()
plt.show()

Correlation Matrix

Let’s assume that just like the Michigan series, the California and Florida time series are also stationary. With this assumption, let’s compute the correlation matrix of these three series.

correlation_matrix = usa_unrate.corr()
print(correlation_matrix)

            california  michigan   florida
california    1.000000  0.944712  0.957694
michigan      0.944712  1.000000  0.948046
florida       0.957694  0.948046  1.000000

It seems like they are strongly and positively correlated with each other!

ARIMA Modelling (single variable)

Since our time series is stationary, we can apply ARIMA model to forecast the Michigan unemployment rate!

For the order paramater, we will input 1, 0, 1 for p (autoregressive term or AR), d (differencing), and q (moving average term or MA). d is 0 here because we’ve ascertained in the previous slide that our time series is stationary.

mi_model = tsa.ARIMA(usa_unrate['michigan'], order=(1,0,1)).fit() 
print(mi_model.summary())

ARIMA Modelling (single variable)

                               SARIMAX Results                                
==============================================================================
Dep. Variable:               michigan   No. Observations:                  132
Model:                 ARIMA(1, 0, 1)   Log Likelihood                -254.685
Date:                Thu, 10 Oct 2024   AIC                            517.371
Time:                        16:37:12   BIC                            528.902
Sample:                    01-01-2013   HQIC                           522.056
                         - 12-01-2023                                         
Covariance Type:                  opg                                         
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
const          5.7663      1.922      3.000      0.003       1.999       9.534
ar.L1          0.7556      0.143      5.277      0.000       0.475       1.036
ma.L1          0.0695      0.264      0.263      0.793      -0.449       0.588
sigma2         2.7560      0.184     14.990      0.000       2.396       3.116
===================================================================================
Ljung-Box (L1) (Q):                   0.00   Jarque-Bera (JB):             72308.74
Prob(Q):                              0.96   Prob(JB):                         0.00
Heteroskedasticity (H):               0.85   Skew:                            10.42
Prob(H) (two-sided):                  0.61   Kurtosis:                       115.75
===================================================================================

Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).

ARIMA - potential interpretation

The constant terms is statistically significant, indicating a base unemployment level of around 5.77%. The ar.L1 is statistically significant (p < 0.05), which indicates strong autocorrelation with previous month’s rate. However, the ma.L1 is not statistically significant (p = 0.79), which suggests that this component may not be necessary for our model. Residuals diagnostics indicates that the residuals is homoeskedastic, but the high skewness and kurtosis indicates that there may be outliers.

Since the MA component may not be necessary, we should consider re-running ARIMA with 1, 0, 0 order.

Now that we have our ARIMA model, let’s use it to forecast future values of unemployment rate in Michigan.

Forecast future value

Let’s predict the unemployment rate for Michigan for the next 6 months from the end of the time series.

mi_forecast = mi_model.get_forecast(steps=6)
print(mi_forecast.predicted_mean)

2024-01-01    4.481162
2024-02-01    4.795229
2024-03-01    5.032543
2024-04-01    5.211861
2024-05-01    5.347357
2024-06-01    5.449740
Freq: MS, Name: predicted_mean, dtype: float64

Confidence Intervals of forecast

Let’s see the confidence intervals of the forecast.

print(mi_forecast.conf_int())

            lower michigan  upper michigan
2024-01-01        1.227412        7.734912
2024-02-01        0.576927        9.013531
2024-03-01        0.351832        9.713253
2024-04-01        0.286567       10.137155
2024-05-01        0.287716       10.406998
2024-06-01        0.314969       10.584510

Prediction instead of forecast

We could also try to get our model to predict values within the sample (i.e. in-sample testing). Let’s see the model’s prediction for 2014.

prediction = mi_model.predict(start=12, end=23)

print(prediction)

2014-01-01    7.633507
2014-02-01    7.562088
2014-03-01    7.484541
2014-04-01    7.407419
2014-05-01    7.247760
2014-06-01    7.093834
2014-07-01    7.022019
2014-08-01    6.861991
2014-09-01    6.708091
2014-10-01    6.553765
2014-11-01    6.399469
2014-12-01    6.245171
Freq: MS, Name: predicted_mean, dtype: float64

print(usa_unrate.loc['2014', 'michigan'])

2014-01-01    8.1
2014-02-01    8.0
2014-03-01    7.9
2014-04-01    7.7
2014-05-01    7.5
2014-06-01    7.4
2014-07-01    7.2
2014-08-01    7.0
2014-09-01    6.8
2014-10-01    6.6
2014-11-01    6.4
2014-12-01    6.2
Name: michigan, dtype: float64

Section 3: Putting it all together

Pick an indicator and analyze or visualize it!

Use the fredapi wrapper to search FRED for a suitable data of your own choosing
Clean and visualize the data with seaborn
Use statsmodels package to perform a suitable analysis of your choice.
Present to the class!

Key things to remember

Organize your files and folders neatly: A tidy workspace enhances productivity by reducing potential sources of error, such as “file not found” bugs.
Familiarize yourself with essential packages: While there are many packages available, certain core libraries like numpy, pandas, matplotlib, seaborn, and statsmodels are must-haves for data analysis.
Always check the documentation: Every API is different, so do consult the documentation to understand how to use it correctly.
The most common type of errors are typo errors.

Thank you for your participation! 😄

All the best for your studies!

(Manifesting academic prosperity and high-paying job after graduation to everyone who attended the workshop!)

If you need help with Python, my email is bellar@smu.edu.sg

Post-workshop survey

Please scan this QR code or click on the link below to fill in the post-workshop survey. It should not take more than 2-3 minutes.

Survey link: https://smusg.asia.qualtrics.com/jfe/form/SV_0VeOJo3H5bWy7P0

Introduction to APIs and statsmodels

Recap from last week

Overview for today

Section 1: Application Programming Interface (API)

What is it?

How to do it in Python

What does a JSON look like?

Federal Reserve Economic Data (FRED) API

Best Practice: How to store your API key

Reading the api key from plain text

Interacting with FRED API

Anatomy of an API request

Check out the result!

Sieve results and save to CSV

The easier way: FRED API wrapper, fredapi package

The easier way: FRED API wrapper, fredapi package

Merging two (or more) dataframes

Merging two (or more) dataframes

Plot them!

More APIs to try

Learning Check

Section 2: The statsmodel package

Introduction and where to find the guides

Let’s try a simple regression - OLS

Let’s try a simple regression - OLS

OLS from formula sub-package

OLS from formula sub-package

Let’s try some Time Series analysis

Stationarity test (ADF)

Seasonal Decomposition

Seasonal Decomposition

Individually retrieve trends, season, and residuals

Correlation Matrix

ARIMA Modelling (single variable)

ARIMA Modelling (single variable)

ARIMA - potential interpretation

Forecast future value

Confidence Intervals of forecast

Prediction instead of forecast

Section 3: Putting it all together

Key things to remember

Thank you for your participation! 😄

Post-workshop survey

The easier way: FRED API wrapper, `fredapi` package

The easier way: FRED API wrapper, `fredapi` package

OLS from `formula` sub-package

OLS from `formula` sub-package