Basic Inferential Stats in R: Correlation, T-Tests, and ANOVA

Bella Ratmelia

Today’s Outline

Refreshers on data distribution and research variables
Statistical tests: chi-square, t-test, correlations.
ANOVA

Refresher: Data Distribution

The choice of appropriate statistical tests and methods often depends on the distribution of the data. Understanding the distribution helps in selecting the right and validity of the tests.

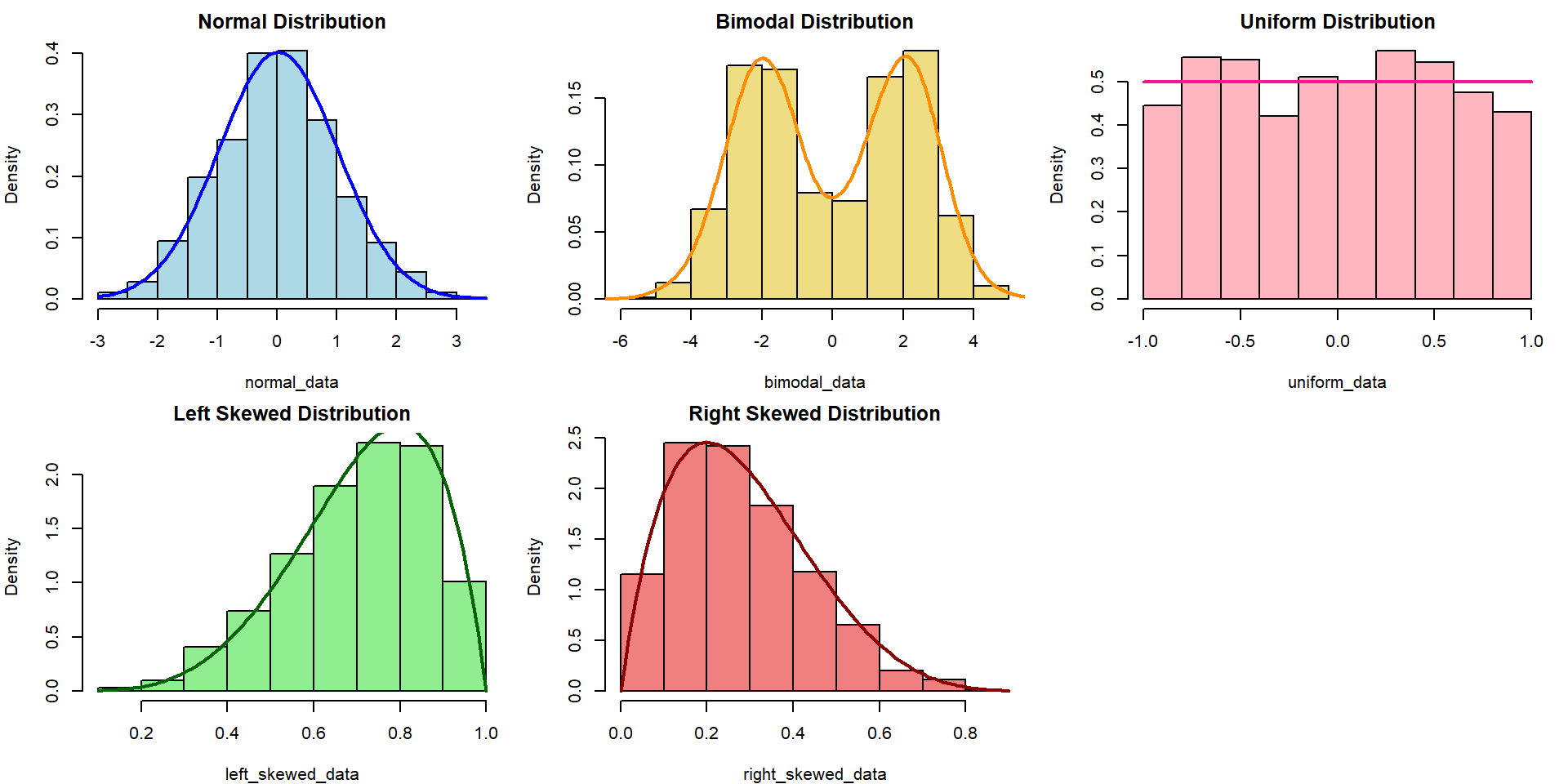
Refresher: Research Variables

Dependent Variable (DV)

The variables that will be affected as a result of manipulation/changes in the IVs

Other names for it: Outcome, Response, Output, etc.
Often denoted as \(y\)

Independent Variable (IV)

The variables that researchers will manipulate.

Other names for it: Predictor, Covariate, Treatment, Regressor, Input, etc.
Often denoted as \(x\)

Load our data for today!

Use read_csv from readr package (part of tidyverse) to load our data into a dataframe

# import tidyverse library
library(tidyverse)

# read the CSV with Chile voting data
chile_data <- read_csv("data-output/chile_voting_processed.csv")

chile_data <- chile_data |> 
    mutate(across(c("region", "sex", "education", "vote", "age_group", "support_level"), as.factor))

#reordering
chile_data <- chile_data |> 
    mutate(education = factor(education, 
                         levels = c("P", "S", "PS"), 
                         ordered = TRUE))

# peek at the data, pay attention to the data types!
glimpse(chile_data)

Chi-square test of independence

The \(X^2\) test of independence evaluates whether there is a statistically significant relationship between two categorical variables.

This is done by analyzing the frequency table (i.e., contingency table) formed by two categorical variables.

Example: Is there any relationship between education and vote in our Chile voting data?

Typically, we can start with visualizing the data first!

    
       A   N   U   Y
  P   49 262 282 409
  S   98 385 223 304
  PS  30 220  46 123

Chi-Square: Sample problem and results

Is there any relationship between education and vote in our Chile voting data?

chisq.test(table(chile_data$education, chile_data$vote))


    Pearson's Chi-squared test

data:  table(chile_data$education, chile_data$vote)
X-squared = 135.69, df = 6, p-value < 2.2e-16

X-squared = the coefficient
df = degree of freedom
p-value = the probability of getting more extreme results than what was observed. Generally, if this value is less than the pre-determined significance level (also called alpha), the result would be considered “statistically significant”

What if there is a hypothesis? How would you write this in the report?

Correlation

A correlation test evaluates the strength and direction of a linear relationship between two variables. The coefficient is expressed in value between -1 to 1, with 0 being no correlation at all.

Pearson’s \(r\) (r)

Measure the association between two continuous numerical variables
Sensitive to outliers
Assumes normality and/or linearity
(most likely the one that you learned in class)

Kendall’s \(\tau\) (tau)

Measure the association between two variables (ordinal-ordinal or ordinal-continuous)
less sensitive/more robust to outliers
non-parametric, does not assume normality and/or linearity

Spearman’s \(\rho\) (rho)

Measure the association between two variables (ordinal-ordinal or ordinal-continuous)
less sensitive/more robust to outliers
non-parametric, does not assume normality and/or linearity

For more info, you can refer to this reading: Measures of Association - How to Choose? (Harry Khamis, PhD)

Correlation: Sample problem and result

RQ: Is there a significant correlation between a respondent’s age and statusquo?

As both variables are numerical and continuous, we can use pearson correlation.

Let’s start with visualizing the data, which can be used to support the explanation.

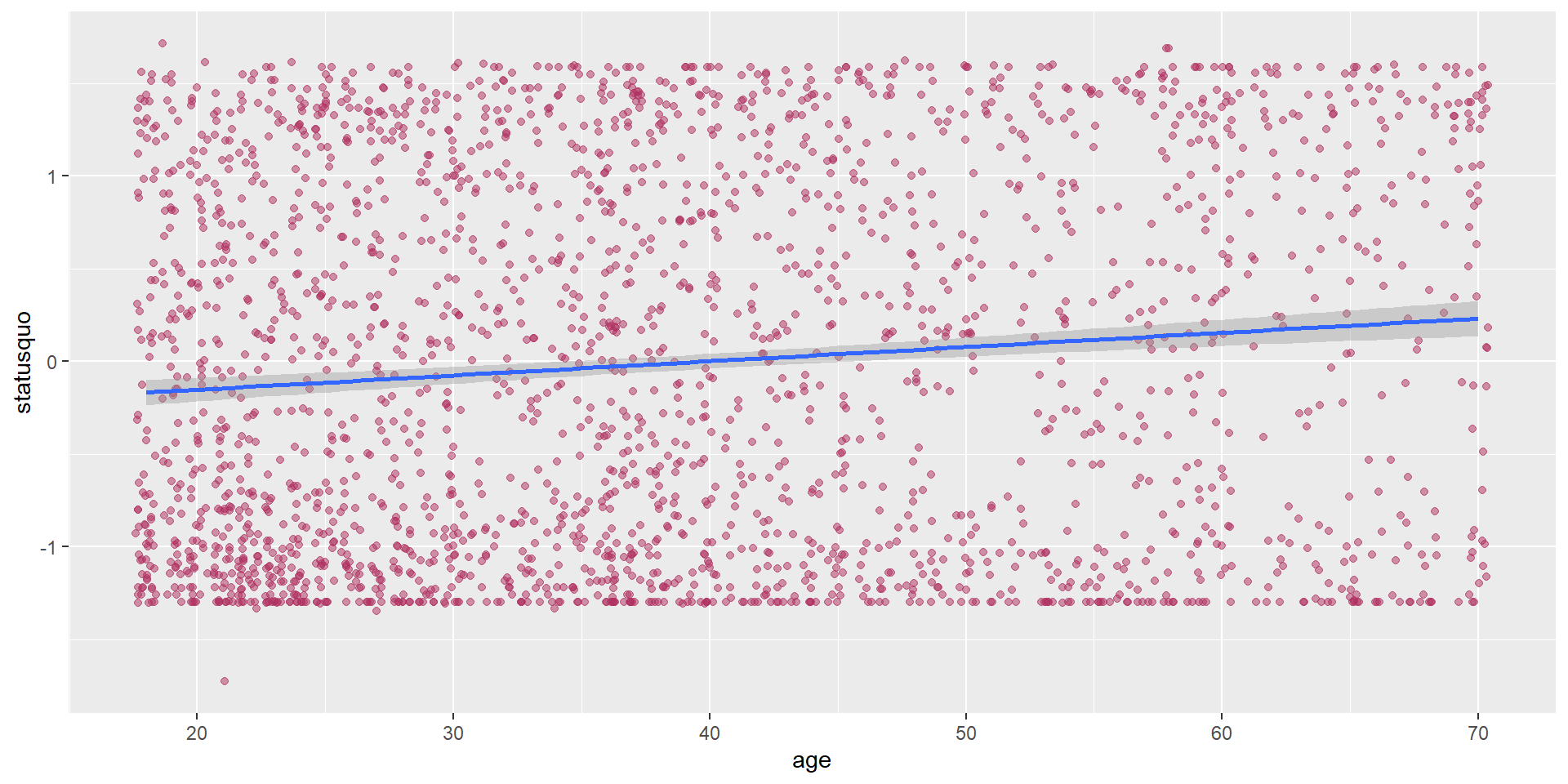
Conduct the correlation test

cor.test(chile_data$age, chile_data$statusquo, 
         method = "pearson")


    Pearson's product-moment correlation

data:  chile_data$age and chile_data$statusquo
t = 5.5546, df = 2429, p-value = 3.086e-08
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 0.07256203 0.15107687
sample estimates:
      cor 
0.1119942

cor is the correlation coefficient - this is the number that you want to report.
t is the t-test statistic
df is the degrees of freedom
p-value is the significance level of the t-test
conf.int is the confidence interval of the coefficient at 95%
sample estimates is the correlation coefficient

Let’s try this correlation exercise! (5 mins)

Calculate the correlation coefficient between age and income
- Which method should you use for this?
- How strong is the correlation? i.e. would you say it’s a strong correlation?
- In which direction is the correlation?
- Is the correlation coefficient statistically significant?
- Visualize the relationship!

T-Tests

A t-test is a statistical test used to compare the means of two groups/samples of continuous data type and determine if the differences are statistically significant.

The Student’s t-test is widely used when the sample size is reasonably small (less than approximately 30) or when the population standard deviation is unknown.

3 types of t-test

One-sample T-test

Test if a specific sample mean (X̄) is statistically different from a known or hypothesized population mean (μ or mu)

Two-samples / Independent Samples T-test

Used to compare the means of two independent groups (such as between-subjects research) to determine if they are significantly different.

Examples: Men vs Women group, Placebo vs Actual drugs.

Paired Samples T-Test

Used to compare the means of two related groups, such as repeated measurements on the same subjects (within-subjects research).

Examples: Before workshop vs After workshop.

T-test: One-sample T-Test

RQ: Is the average age of participants who intend to vote “Yes” significantly greater than the overall mean age of voting population in Chile? Assume the population mean is 35.

Let’s start with visualizing the data

yes_voters_age <- chile_data |>
    filter(vote == "Y") |>
    select(age)   


yes_voters_age |> 
    ggplot(aes(y = age, x = 1)) +
    geom_boxplot(width = 0.2) + 
    geom_hline(yintercept = 35, color="red") +
    geom_label(label = "population mean", 
               x = 1, y = 35.1, 
               label.size = 0.15) +
    coord_flip() +
    theme(aspect.ratio = 1/3)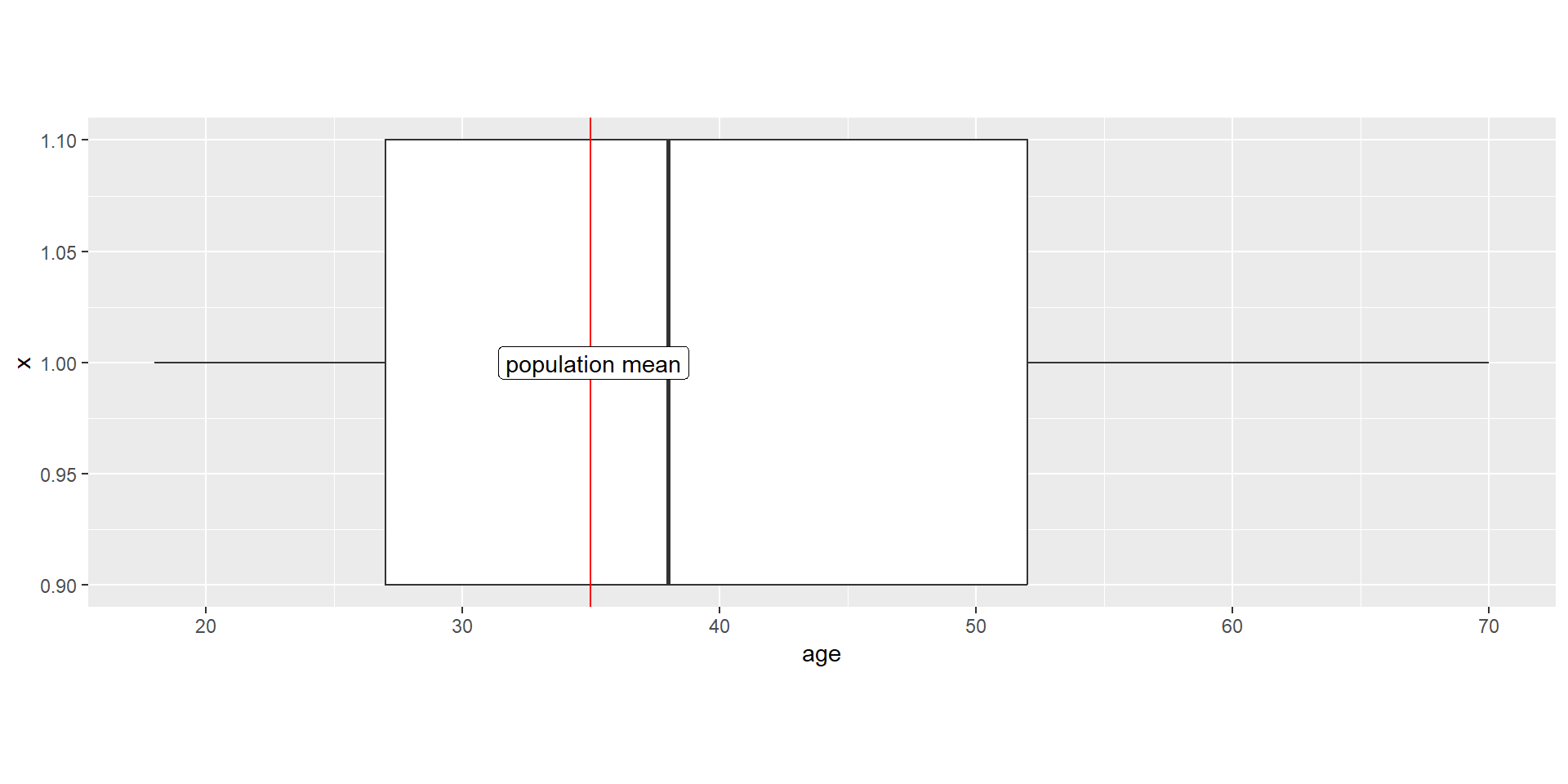

Conduct the One-sample T-Test

population_mean_age = 35  

t.test(yes_voters_age,          
       alternative = "greater", 
       mu = population_mean_age)


    One Sample t-test

data:  yes_voters_age
t = 9.9302, df = 835, p-value < 2.2e-16
alternative hypothesis: true mean is greater than 35
95 percent confidence interval:
 39.3405     Inf
sample estimates:
mean of x 
 40.20335

What if there is a hypothesis? How would you write this in the report?

T-Test: Independent Samples T-Test

RQ: Is there a significant difference in age between those who intend to vote “Yes” and those who intend to vote “No”?

Let’s first take only the necessary columns and get some summary statistics, particularly on the number of samples for each group, as well as the mean, standard deviation, and variance.

voters_age <- chile_data |> 
    select(age, vote) |> 
    filter(vote == "Y" | vote == "N") 

voters_age |> 
    group_by(vote) |> 
    summarise(total = n(), 
              mean = mean(age),
              variance = var(age),
              stdeviation = sd(age))

# A tibble: 2 × 5
  vote  total  mean variance stdeviation
  <fct> <int> <dbl>    <dbl>       <dbl>
1 N       867  36.0     205.        14.3
2 Y       836  40.2     230.        15.2

Visualize the differences between two samples

The variance will be easier to see when we visualize it as well. As we can see, the variance for Y group is wider than the N group. This suggests that the variance might be heterogeneous (heteroskedastic).

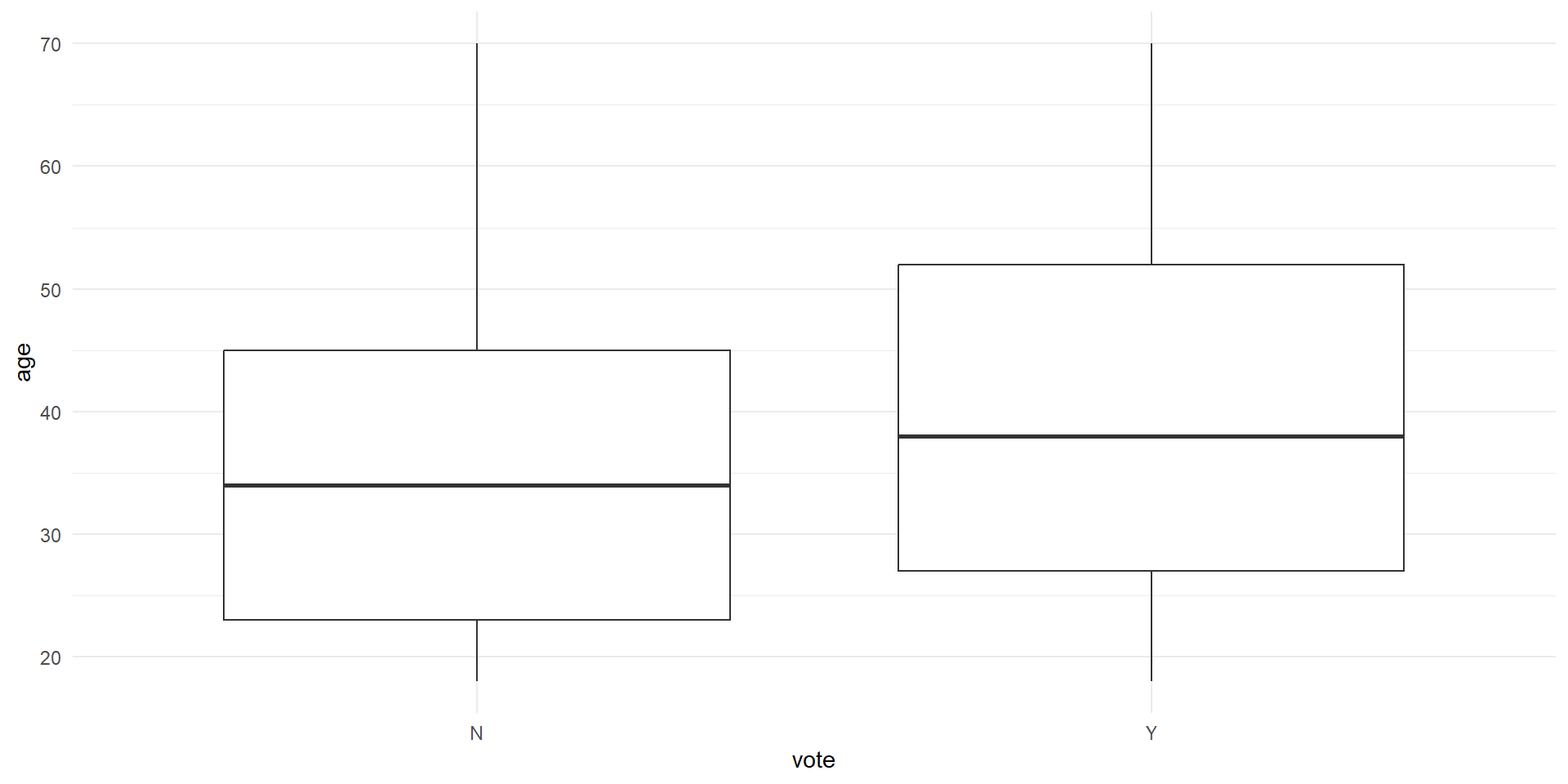
Conduct the independent samples T-test

Remember, the hypotheses are:

\(H_0\): There is no significant difference in the mean age between those who intend to vote “Yes” and those who intend to vote “No”.

\(H_1\): There is a significant difference in the mean age between those who intend to vote “Yes” and those who intend to vote “No”.

t.test(age ~ vote, 
       data = voters_age, 
       var.equal = FALSE)


    Welch Two Sample t-test

data:  age by vote
t = -5.8797, df = 1686.7, p-value = 4.944e-09
alternative hypothesis: true difference in means between group N and group Y is not equal to 0
95 percent confidence interval:
 -5.607052 -2.801954
sample estimates:
mean in group N mean in group Y 
       35.99885        40.20335

Notice that we are using Welch’s t-test instead of Students’ t-test

Welch’s t-test (also known as unequal variances t-test, is a more robust alternative to Student’s t-test. It is often used when two samples have unequal variances and possibly unequal sample sizes.

T-Test: Paired Sample T-Test

Unfortunately, our data is not suitable for paired T-Test. For demo purposes, we are going to use a built-in sample datasets called sleep from the base R dataset.

The dataset is already loaded, so you can use it right away!

type View(sleep) in your R console (bottom left), and then press enter. RStudio will open up the preview of the dataset.
type ?sleep in your R console to view the help page (a.k.a vignette) about this dataset.
type data() in your console to see what are the available datasets that you can use for practice!

Rows: 20
Columns: 3
$ extra <dbl> 0.7, -1.6, -0.2, -1.2, -0.1, 3.4, 3.7, 0.8, 0.0, 2.0, 1.9, 0.8, …
$ group <fct> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2
$ ID    <fct> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10

Visualise the before (group 1) and after (group 2)

# A tibble: 2 × 5
  group     n  mean    sd variance
  <fct> <int> <dbl> <dbl>    <dbl>
1 1        10  0.75  1.79     3.20
2 2        10  2.33  2.00     4.01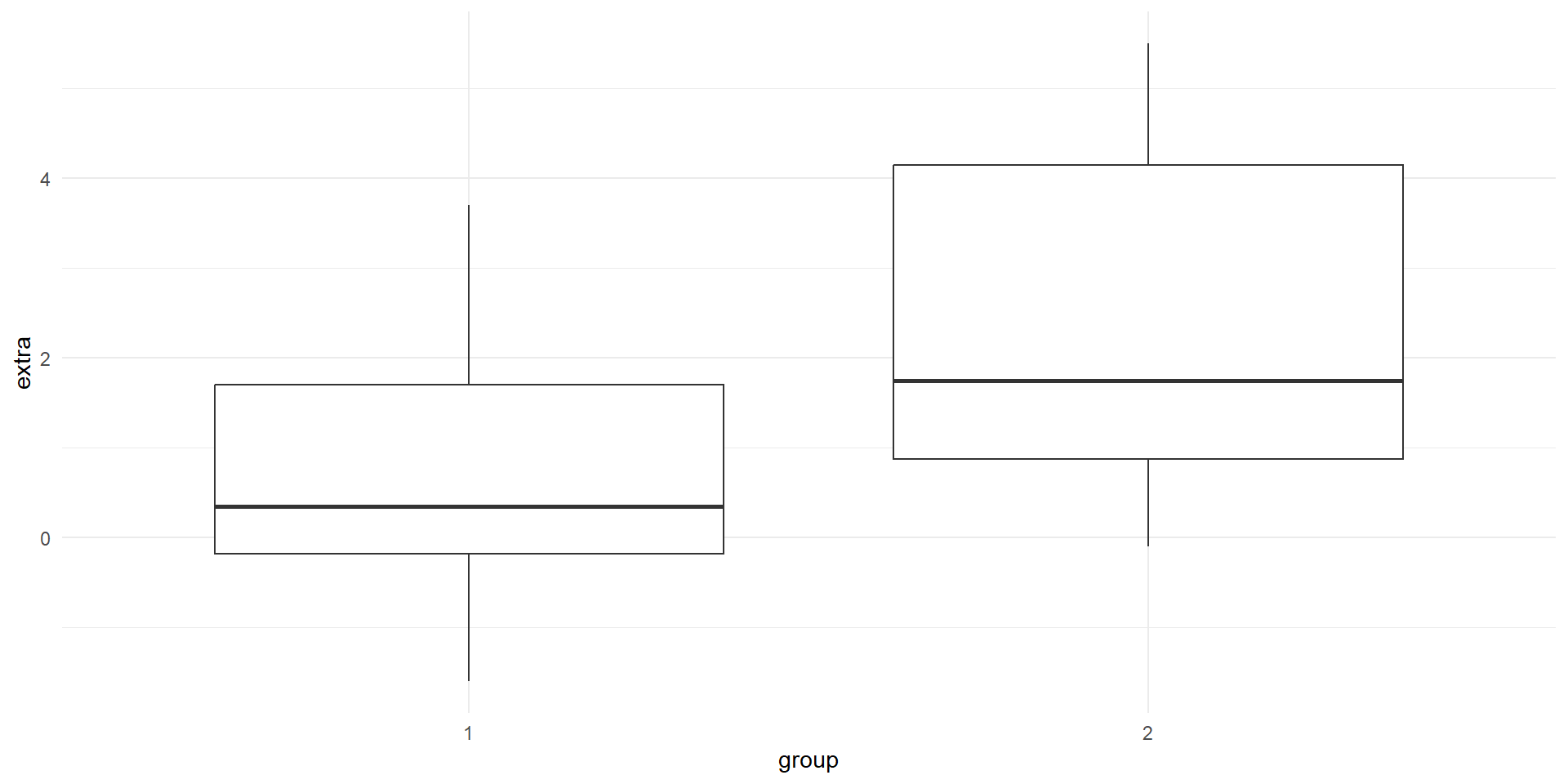

Transform the data shape

The data is in long format. let’s transform it into wide format so that we can conduct the analysis more easily.

sleep_wide <- sleep |> 
    pivot_wider(names_from = group, values_from = extra, 
                names_prefix = "group_")
glimpse(sleep_wide)

Rows: 10
Columns: 3
$ ID      <fct> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
$ group_1 <dbl> 0.7, -1.6, -0.2, -1.2, -0.1, 3.4, 3.7, 0.8, 0.0, 2.0
$ group_2 <dbl> 1.9, 0.8, 1.1, 0.1, -0.1, 4.4, 5.5, 1.6, 4.6, 3.4

Conduct the paired-sample T-test

Remember, the hypotheses are:

\(H_0\): There is no significant difference in the increase in hours of sleep.

\(H_1\): There is a significant difference in the increase in hours of sleep.

t.test(Pair(sleep_wide$group_1, sleep_wide$group_2) ~ 1,
       data = sleep)


    Paired t-test

data:  Pair(sleep_wide$group_1, sleep_wide$group_2)
t = -4.0621, df = 9, p-value = 0.002833
alternative hypothesis: true mean difference is not equal to 0
95 percent confidence interval:
 -2.4598858 -0.7001142
sample estimates:
mean difference 
          -1.58

ANOVA (Analysis of Variance)

ANOVA (Analysis of Variance) is a statistical test used to compare the means of three or more groups or samples and determine if the differences are statistically significant.

There are two ‘mainstream’ ANOVA that will be covered in this workshop:

One-Way ANOVA: comparing means across two or more independent groups (levels) of a single independent variable.
Two-Way ANOVA: comparing means across two or more independent groups (levels) of two independent variable.
Other types of ANOVA that you may encounter: Repeated measures ANOVA, Multivariate ANOVA (MANOVA), ANCOVA, etc.

One-Way ANOVA: Sample problem and result

RQ: Is there a significant difference in statusquo scores between different education levels?

Let’s visualize the data first!

Conduct the one-way Anova test

statusquo_edu_anova <- aov(statusquo ~ education, data = chile_data)
summary(statusquo_edu_anova)

              Df Sum Sq Mean Sq F value   Pr(>F)    
education      2   51.2  25.583   25.87 7.63e-12 ***
Residuals   2428 2401.0   0.989                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

F-value: the coefficient value
Pr(>F): the p-value
Sum Sq: Sum of Squares
Mean Sq : Mean Squares
Df: Degrees of Freedom

Post-hoc test (only when result is significant)

If your ANOVA test indicates significant result, the next step is to figure out which category pairings are yielding the significant result.

Tukey’s Honest Significant Difference (HSD) can help us figure that out! Other alternative is the pairwise.t.test, but let’s try Tukey’s for now.

TukeyHSD(statusquo_edu_anova)

  Tukey multiple comparisons of means
    95% family-wise confidence level

Fit: aov(formula = statusquo ~ education, data = chile_data)

$education
           diff        lwr         upr     p adj
S-P  -0.2465701 -0.3505516 -0.14258851 0.0000001
PS-P -0.3674205 -0.5030933 -0.23174756 0.0000000
PS-S -0.1208504 -0.2563647  0.01466399 0.0918081

ANOVA Assumptions

The Dependent variable should be a continuous variable
The Independent variable should be a categorical variable
The observations for Independent variable should be independent of each other
The Dependent Variable distribution should be approximately normal – even more crucial if sample size is small.
- You can verify this by visualizing your data in histogram, or use Shapiro-Wilk Test, among other things
The variance for each combination of groups should be approximately equal – also referred to as “homogeneity of variances” or homoskedasticity.
- One way to verify this is using Levene’s Test
No significant outliers

Verifying the assumption: Test for Homogeneity of variance

Levene’s Test to test for homogeneity of variance i.e. homoskedasticity

library(car)
leveneTest(income ~ education, 
           data = chile_data)

Levene's Test for Homogeneity of Variance (center = median)
        Df F value    Pr(>F)    
group    2  164.96 < 2.2e-16 ***
      2428                      
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

The results indicate that the p-value is less than the significance level of 0.05, suggesting a significant difference in variance across the groups. Consequently, the assumption of homogeneity of variances is violated.

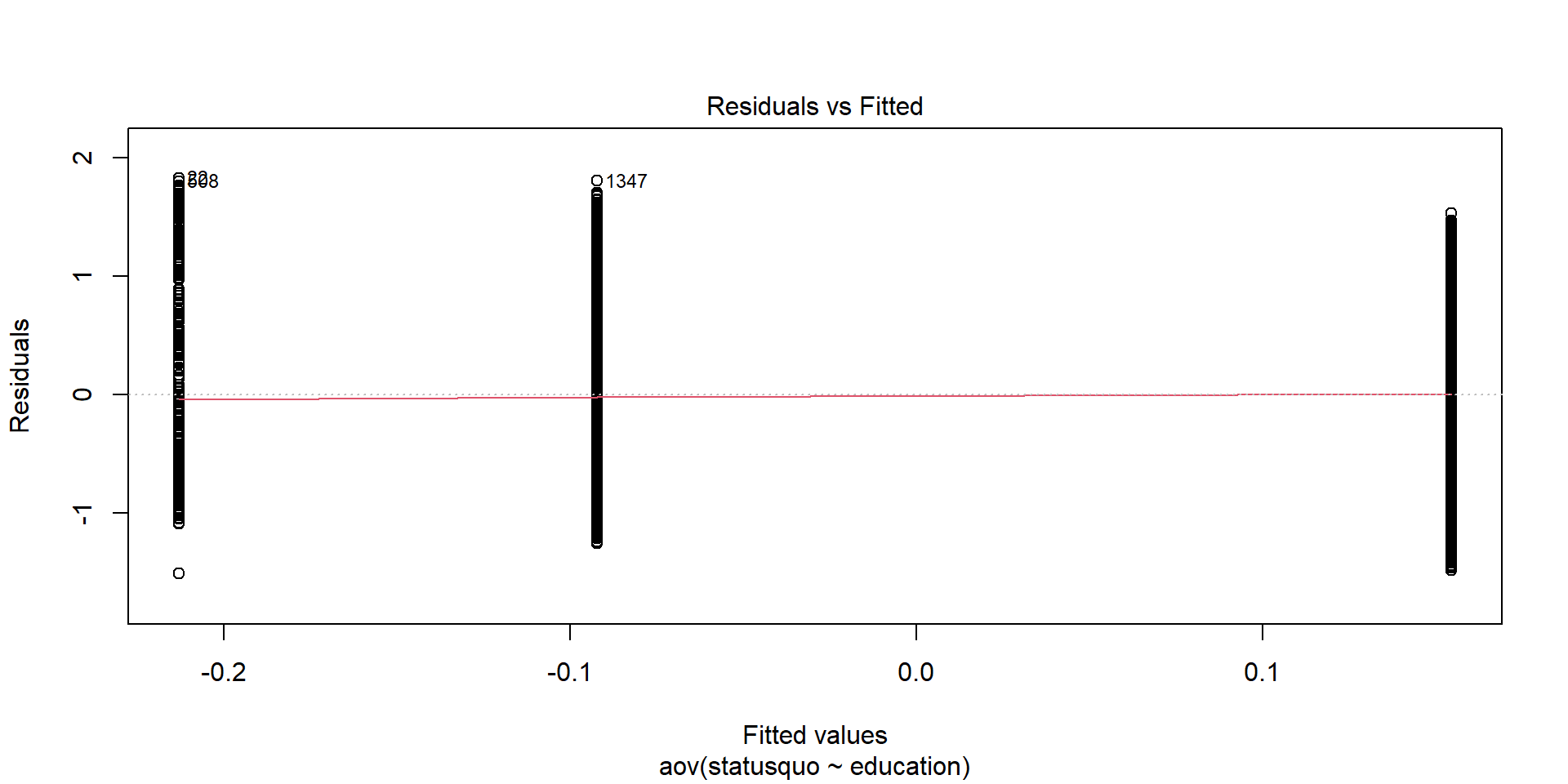
Plotting Residuals: Residual vs Fitted

When we plot the residuals¹, we can see some outliers as well:

Verifying the assumptions: Test for Normality

Shapiro-Wilk Test to test for normality.

library(car)
shapiro.test(chile_data$income)


    Shapiro-Wilk normality test

data:  chile_data$income
W = 0.66002, p-value < 2.2e-16

The p-value from the Shapiro-Wilk test is less than the significance level of 0.05, indicating that the data significantly deviates from normality. Therefore, the assumption of normality is not satisfied.

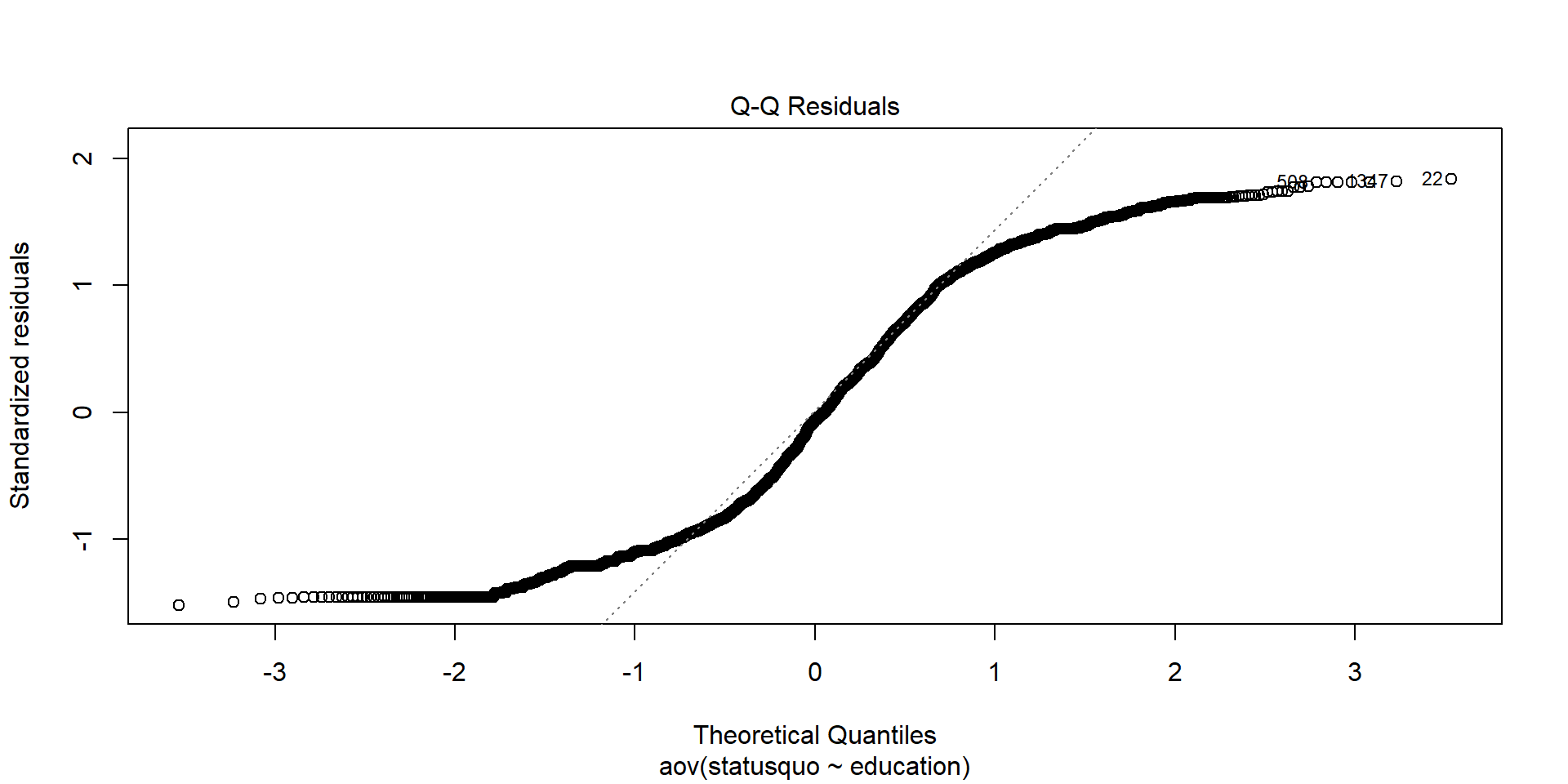
Plotting Residuals: Q-Q Plot

We can see this better from when we plot the residuals:

When the assumptions are not met…

We can use Kruskal-Wallis rank sum test as an non-parametric alternative to One-Way ANOVA!

kruskal.test(statusquo ~ education, data = chile_data)


    Kruskal-Wallis rank sum test

data:  statusquo by education
Kruskal-Wallis chi-squared = 43.324, df = 2, p-value = 3.91e-10

Other alternative: Welch’s ANOVA for when the homoskedasticity assumption is not met.

oneway.test(statusquo ~ education, data = chile_data, var.equal = FALSE)


    One-way analysis of means (not assuming equal variances)

data:  statusquo and education
F = 25.205, num df = 2.0, denom df = 1143.3, p-value = 1.942e-11

Two-Way ANOVA: Sample problem and result

RQ: Is there a significant difference in statusquo scores between different education levels and sexes?

Let’s visualize the data!

Conduct the Two-way ANOVA test

statusquo_edu_sex_anova <- aov(statusquo ~ education + sex, data = chile_data)
summary(statusquo_edu_sex_anova)

              Df Sum Sq Mean Sq F value  Pr(>F)    
education      2   51.2  25.583   25.94 7.1e-12 ***
sex            1    7.7   7.692    7.80 0.00526 ** 
Residuals   2427 2393.3   0.986                    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Post-hoc test for Two-way ANOVA

TukeyHSD(statusquo_edu_sex_anova)

  Tukey multiple comparisons of means
    95% family-wise confidence level

Fit: aov(formula = statusquo ~ education + sex, data = chile_data)

$education
           diff        lwr         upr     p adj
S-P  -0.2465701 -0.3504064 -0.14273380 0.0000001
PS-P -0.3674205 -0.5029038 -0.23193712 0.0000000
PS-S -0.1208504 -0.2561754  0.01447465 0.0912018

$sex
          diff        lwr         upr     p adj
M-F -0.1121996 -0.1912197 -0.03317946 0.0054057

Let’s try this ANOVA exercise! (5 mins)

Is there a significant difference in income between different regions and statusquo?

Visualize the data as well
Test for normality and homoskedasticity, and choose the appropriate test

End of Session 4!

Next session: Linear and Logistic Regressions!